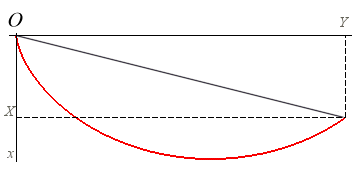
En orientant l'axe des x vers le bas, le temps de descente le long d'une courbe de (0, 0) à (X, Y) est proportionnel à
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE SYNODALE
Synodal
curve, synodale Kurve
| Courbe étudiée par Bonati en 1780.
Du grec syn "avec" et odos "chemin". |
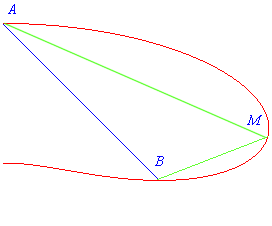
Deux courbes joignant un point A à un point
B,
placées dans un champ de pesanteur uniforme sont dites
synodales
si, lorsqu'on lâche en A un point matériel sans vitesse
initiale, les deux points arrivent en même temps en
B, qu'ils
suivent l'une ou l'autre courbe.
| Exemple : les courbes coudées [A=(0,0),
M=(x,y)
, B=(1,1)] qui sont synodales de la ligne droite [(0,0), (1,1)]
, sont telles que le lieu de M a pour équation |
 |
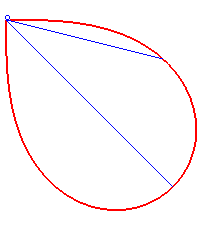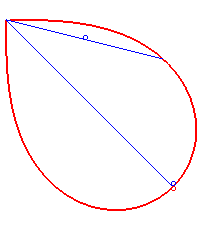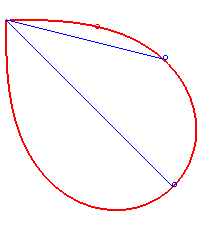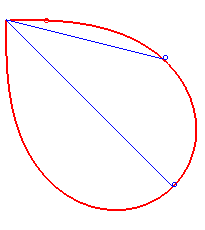
| Bonati a posé et résolu en 1780 le problème de déterminer une courbe issue de O telle qu'à tout instant, le temps mis pour arriver au point M en suivant cette courbe est le même que celui que mettrait un point matériel astreint en partant de O sans vitesse à suivre la droite (OM). Autrement dit, de déterminer une courbe qui soit synodale de toutes ses sécantes issues d'un de ses points. La réponse est une demi lemniscate de Bernoulli. |
 |
| Démonstration du résultat de Bonati :
En orientant l'axe des x vers le bas, le temps de descente le long d'une courbe de (0, 0) à (X, Y) est proportionnel à |
 |
Voir aussi à synchrone,
isochrone
de Huygens, isochrone
de Leibniz, isochrone
de Varignon, brachistochrone
et tautochrone.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2020