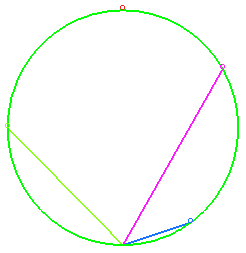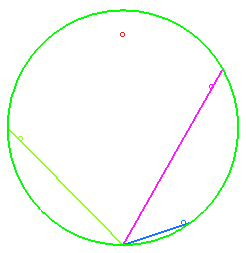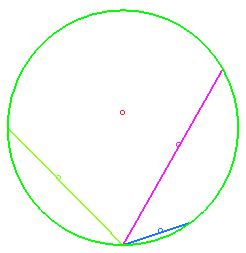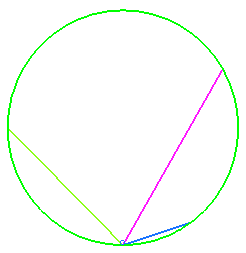
Étant donnés une famille de droites sécantes O et placées dans un champ de pesanteur uniforme, des points matériels pesants glissent sans frottement sur chacune des courbes ; Galilée a posé le problème de savoir sur quelle courbe devait se trouver les points, de sorte que, partant sans vitesse initiale, ils arrivent simultanément en O ; la réponse est un cercle dont le point le plus bas est O.

O

On en déduit que si les points partent de O sans vitesse initiale sur des droites issues de O, la courbe qu'ils forment à chaque instant est également un cercle.

Si l'on remplace les droites par une famille de courbes passant par O, les points étant soumis à la condition de passer simultanément en O, la courbe qu'ils forment à chaque instant est appelée courbe synchrone.

Exemple :
Si les courbes sont des cycloïdes de base horizontale et ayant un point de rebroussement en O, les points partant sans vitesse de O, les courbes synchrones sont les trajectoires orthogonales de ces cycloïdes (Jean Bernoulli).

Voir aussi à synodale, isochrone de Huygens, isochrone de Leibniz, isochrone de Varignon, brachistochrone et tautochrone.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2005