Deux familles de courbes sont dites orthogonales lorsqu'en tout point commun à une courbe de chaque famille, les tangentes sont orthogonales, et l'on dit que l'une des familles est formée des trajectoires orthogonales de l'autre. On est alors en présence d'un système double orthogonal de courbes.
 

	Si la première famille de courbes est donnée sous la forme :	les trajectoires orthogonales sont données par :
Définition géométrique	f( M ) = cte	g (M) = cte avec
Équation implicite cartésienne	P(x, y) = cte	Q(x, y ) = cte avec
Équation implicite cartésienne harmonique	P(x, y) = cte avec P harmonique	Q(x, y ) = cte avec
Equation implicite complexe	Re (f (z) ) = cte avec f holomorphe (donc conforme)	Im (f (z) ) = cte
Équation implicite polaire	P() = cte	Q() = cte avec
Équation différentielle cartésienne	y' = f(x, y)	y' = -1 / f(x, y)
Équation différentielle polaire	r' = f()	r' = - r² / f()
Lignes de champ du champ cartésien :	(f(x, y), g(x, y))	(g(x, y), –f(x, y))
Lignes de champ du champ polaire :	(f(), g())	(g(), –f())

Si les deux familles sont données sous une unique forme paramétrique : , u fixé, v variable pour la première famille, v fixé, u variable pour la deuxième, les deux familles sont orthogonales ssi , ce qui est toujours réalisé si P et Q sont les parties réelle et imaginaire d'une fonction holomorphe (fonction réciproque de celle ci-dessus).

Les trajectoires orthogonales d'une famille de droites sont les développantes de l'enveloppe de cette famille ; ce sont donc des courbes parallèles (voir l'exemple 13 ci-dessous).

Exemples :

Définitions Si vous lisez q, c'est en fait theta, et r, c'est en fait rho...	Expression paramétrique commune (courbes rouges : u = cte courbes bleues : v = cte)	Courbes images réciproques des lignes de coordonnées cartésiennes par la transformation conforme f définie par :	Interprétation physique des courbes rouges	Tracé
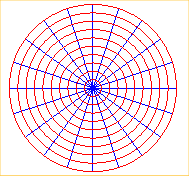
1 courbes 1 (cercles rouges) courbes orthogonales (droites bleues) cartésien polaire équation implicite x² + y² = cte r = a équation différentielle yy' + x = 0 r' = 0 champ (y, -x) (0 , 1) cartésien polaire équation implicite y = kx équation différentielle xy' - y = 0 champ (x, y) (1 , 0)		d'où	Lignes de champ magnétique induit par un courant rectiligne uniforme orthogonal en O à xOy. Équipotentielles électrostatiques induites par une charge placée en O ou des charges uniformément réparties sur une droite orthogonale en O à xOy.
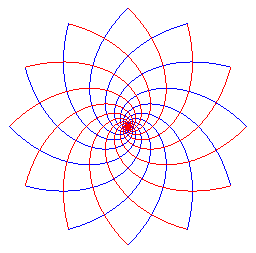
1 bis courbes 1 (spirales logarithmiques: rouges) courbes orthogonales (spirales bleues) cartésien polaire équation implicite équation différentielle (y-x)y' + x +y= 0 champ (x+y, x-y) (1 , 1) cartésien polaire équation implicite équation différentielle (x-y)y' + x +y= 0 champ (x, y) (1 , -1)		d'où
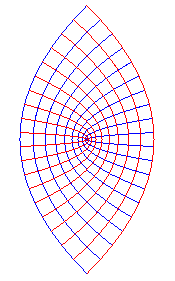
2 Famille de paraboles homofocales courbes 1 (paraboles rouges) courbes orthogonales (paraboles bleues) cartésien polaire équation implicite  y² = 4u²(u²-x) r=2u²/ (1+cos) équation différentielle yy'²+2xy'-y=0 cartésien polaire équation implicite y² = 4v²(v²+x) r=-2v²/ (1+cos) équation différentielle yy'²-2xy'-y=0		d'où
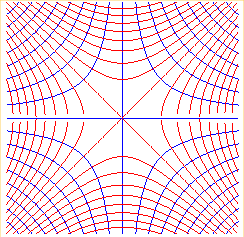
3 courbes 1 (hyperboles rouges) courbes orthogonales (hyperboles bleues) cartésien polaire équation implicite x² - y² = cte r²cos2= cte équation différentielle yy' - x = 0 r' = r tan2q champ (y, x) (sin2, cos2) cartésien polaire équation implicite xy = cte r²sin2= cte  équation différentielle xy' + y = 0 r' = -r cot2 champ (-x, y) (-cos2, sin2)		d'où	Visualisation approchée de l'exemple n° 8 ci-dessous au voisinage de O. Ce sont les courbes de niveau du paraboloïde hyperbolique
4 courbes 1 (cercles rouges) courbes orthogonales (cercles bleus) cartésien polaire équation implicite x² + y² = ax r = a  cos équation différentielle 2xyy' =   y²-x² r' + r  tan = 0 champ (2xy,  y² - x²) (sin, -cos) cartésien polaire équation implicite (x² + y²) = ay r = asin équation différentielle  ( y² - x²) y' + 2xy = 0 r' = r cot champ (x² - y², 2xy) (cos, sin)			Cas limite de l'exemple n°7 ci-dessous quand les conducteurs sont infiniment voisins. Voir ausi l'abaque de Smith.	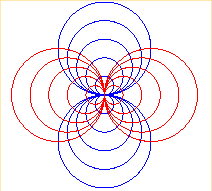= deux faisceaux de cercles singuliers orthogonaux
5 courbes 1 (cardioïdes  rouges) courbes orthogonales (cardioïdes bleues) polaire équation implicite r=acos²/2 équation différentielle r' = r tan /2 champ (sin/2, cos/2) polaire équation implicite r=asin²/2 équation différentielle r' = -r cot/2 champ (-cos/2 , sin/2)			Remarque : figure obtenue par inversion de celle de l'exemple 2.
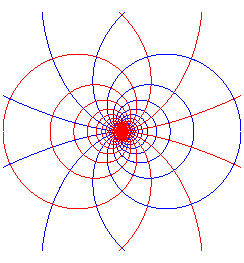6 courbes 1 (spirales sinusoïdales d'indice -n  rouges) courbes orthogonales (spirales sinusoïdales d'indice -n bleues) polaire équation implicite rncosn= cte équation différentielle r' = r tan n champ (sinn, cosn) polaire équation implicite rnsinn= cte  équation différentielle r' = -r cotn champ (-cosn , sinn) les 4 cas précédents correspondent à n = 1/2, n = 2, n = -1 , n =-1/2		d'où	Ci-contre, vues pour n = 4 et n = -4.
7 courbes 1 (oeufs doubles rouges) courbes orthogonales (courbes du dipôle bleues) cartésien polaire équation implicite (x² + y²)3 = a²x4 r = acos²q équation différentielle 3xyy' =  2 y²-x² r' + 2r tan= 0 champ (3xy, 2 y² - x²) (2sin, -cos) cartésien polaire équation implicite (x² + y²)3 = a4y² r² = a²sin équation différentielle  (2y²-x² ) y' + 3xy = 0 2r' = r cot champ (x² - 2 y², 3xy) (cos, 2sin) Remarque : les exemples 4 et 7 font partie de l'exemple plus général des courbes de Clairaut : r = acosn et rn= ansin.	????	????	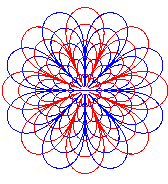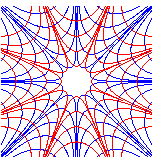Lignes de champ d'un dipôle magnétique Lignes de champ d'un dipôle électrostatique (cas limite, en inversant les courbes rouges et les courbes bleues, de l'exemple n°9 ci-après).
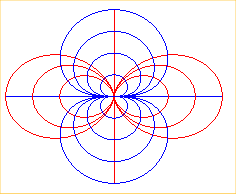8 courbes 1 (cercles d'Apollonius rouges) courbes orthogonales (cercles bleus) définition géométrique MA/MB = cte avec A(1,0) et B(-1,0) équation implicite (x - a)² + y² =  a² - 1 équation différentielle  y' (x² - y² - 1) = 2xy définition géométrique (MA, MB) = cte équation implicite  x² + (y - a)² =  a² + 1  équation différentielle 2xyy' = -x² + y² + 1 champ MA/MA² - MB/MB²		d'où	Lignes de champ magnétique induit par un courant rectiligne uniforme orthogonal en A à xOy et un courant parallèle de sens contraire passant par B. Équipotentielles électrostatiques induites par des charges uniformément réparties sur une droite orthogonale en A à xOy et des charges opposées u. r. sur une droite orthogonale en B à xOy.	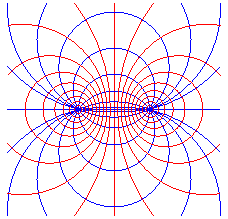= deux faisceaux de cercles orthogonaux
9 courbes 1 (ovales de Cassini rouges) courbes orthogonales (hyperboles équilatères bleues) définition géométrique MA .MB = cte   polaire équation implicite r4 - 2r² cos2= cte équation différentielle r'( r2 - cos2) +rsin2=0 champ (sin2, cos2 - r²) définition géométrique (Ox, AM) + (Ox, BM) = cte champ MA/MA² - MB/MB² polaire équation implicite r² = cos2a / cos(2(-a)) équation différentielle sin2r'= r3 - rcos2 champ (r² - cos2, sin2)		d'où	Lignes de champ magnétique induit par un courant rectiligne uniforme orthogonal en A à xOy et un courant parallèle de même sens passant par B. Équipotentielles électrostatiques induites par des charges uniformément réparties sur une droite orthogonale en A à xOy et des charges égales u. r. sur une droite orthogonale en B à xOy.	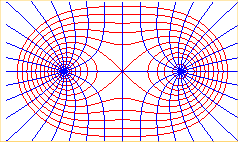Voir une généralisation à cassinienne pour les courbes rouges, et à stelloïde pour les courbes bleues : cas où .
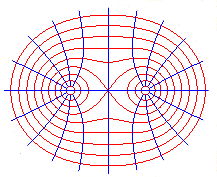
10 courbes 1 (équipotentielles de Cayley rouges) courbes orthogonales (en bleu) définition géométrique 1/MA-1/MB = cte champ définition géométrique champ MA/MA3 - MB/MB3			Équipotentielles électrostatiques induites par deux charges opposées placées en A et en B, autrement dit, un dipôle électrostatique.
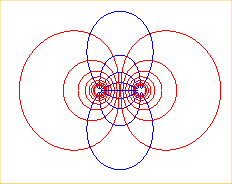11 courbes 1 (ovales de Cayley rouges) courbes orthogonales (en bleu) définition géométrique 1/MA + 1/MB = cte champ définition géométrique champ MA/MA3 + MB/MB3			Équipotentielles électrostatiques induites par deux charges égales placées en A et en B.
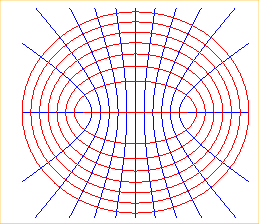
12 Réseau de coniques homofocales courbes 1 (ellipses rouges) courbes orthogonales (hyperboles bleues) définition géométrique MA + MB = cte champ MA/MA - MB/MB équation cartésienne x²/(1+cte)+y²/cte=1 définition géométrique MA - MB  = cte champ MA/MA + MB/MB équation cartésienne x²/(1-cte)-y²/cte=1		f(z) = argch(z) f-1(z) =  ch (z) (image du réseau n°1 par la transformation de Joukovski :  j(z) = (z + 1/z)/2)	Equipotentielles électrostatiques induites par des charges uniformément réparties sur le segment [AB] ??? Figure d'interférence
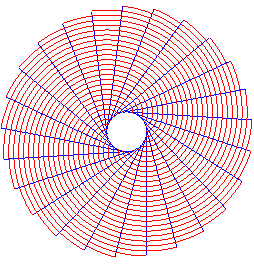
13 Développantes de cercle et leurs génératrices courbes 1 (demi-développantes d'un cercle fixe rouges) courbes orthogonales (demi-tangentes au cercle bleues) paramétrisation complexe paramétrisation complexe	????	????
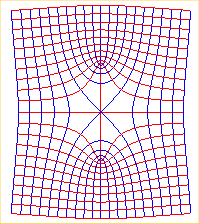
14 courbes 1 (quartiques rouges) courbes orthogonales (quartiques bleues) cartésien équation implicite  y² = a²(1  + 1 / (a²+x²)) paramétrisation x = a tan t y² = a²  + cos²t cartésien équation implicite x² = a²(1 - 1 / (a²+y²)) paramétrisation  x² = a²  - cos²t y = a tan t			Lignes d'écoulement uniforme perturbé par un obstacle (le segment [AB] avec A(0, 1) et B(0, -1))	La courbe bleue passant par O (obtenue pour a = 1) est une puntiforme
15 courbes 1 (hyperboles cubiques rouges) courbes orthogonales (hyperboles cubiques bleues) cartésien équation implicite (y - cte) (x²+y²) = y cartésien équation implicite (x - cte) (x²+y²) + x =0		où j est la transformation de Joukovski	Lignes d'écoulement uniforme perturbé par le dique de centre O et de rayon 1.
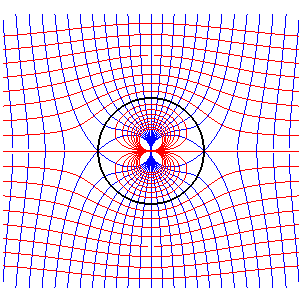16 où . Par exemple, pour v = pi/2, on obtient :			Lignes d'écoulement uniforme dans un tube coudé.

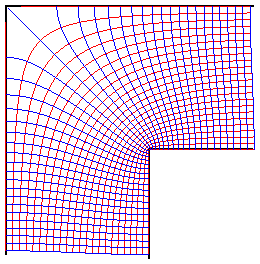Autres exemples :
 

Lemniscates de Bernoulli : et  (cas n = –2 de l'exemple 6 ci-dessus)	Trèfles à 4 feuilles ; et leurs trajectoires orthogonales .
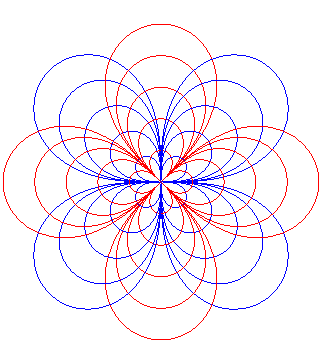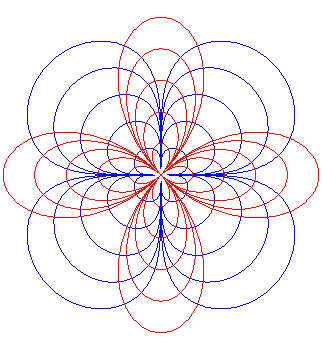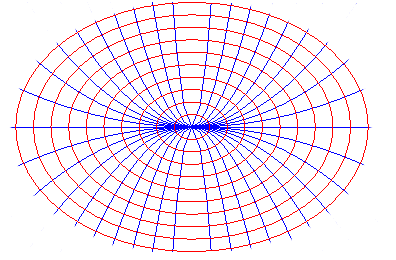
Paraboles  et ellipses	Paraboles rouges  et paraboles semi-cubiques .
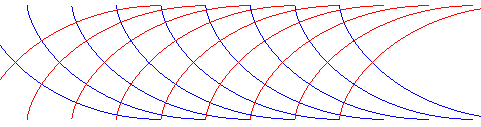
cycloïdes: et cycloïdes symétriques

Voir aussi à tractrice., ainsi que cet article.

Les projections sur un plan horizontal des lignes de pente et des lignes de niveau d'une surface forment deux réseaux orthogonaux ; Voir par exemple la boîte à oeufs.

On peut généraliser la notion de courbes orthogonales à des angles quelconques ; deux familles de courbes se coupent sous l'angle V  lorsqu'en tout point commun à une courbe de chaque famille, les tangentes font un angle V, et l'on dit que l'une des famille est formée des trajectoires sous l'angle V de l'autre.

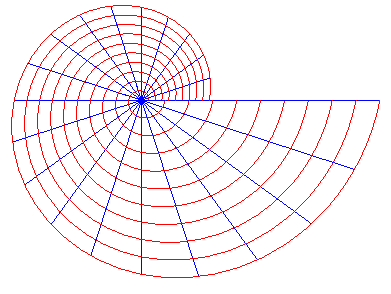
Par exemple, les trajectoires sous l'angle V du faisceau des droites issues de O sont les spirales logarithmiques; :

La généralisation 3D des systèmes doubles orthogonaux est la notion de système triple orthogonal de surfaces.
 
 

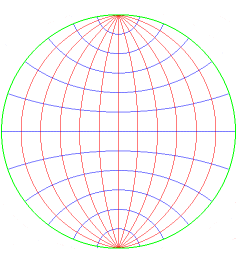
Carte obtenue par projection stéréographique de pôle un point de l'équateur ; les parallèles et méridiens forment deux faisceaux de cercles orthogonaux. Bourse du commerce, Paris.

 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2022