Notion étudiée en 1873 par L'abbé Aoust (p. 119), et en 2010 par Apostol et Mamikon sous le nom de tanvolute. Autres noms : développante oblique, développante généralisée.

 

Si M0 est le point courant de , le point courant M d'une développoïde inverse faisant un angle  avec les tangentes est le lieu des points  où  est défini par l'équation différentielle : , ou  (voir les notations). Cette équation diférentielle linéaire du premier ordre s'intègre en  où .

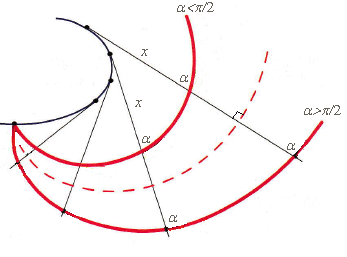
Les développoïdes inverses sous un angle  d'une courbe plane  sont les courbes dont  est la développoïde d'angle . Ce sont donc les courbes traversant sous un angle: les tangentes à la courbe .
Pour  , on retrouve les développantes de .

EXEMPLE : DÉVELOPPOÏDE INVERSE DE CERCLE
 

Pour un cercle de rayon a : paramétrisation cartésienne :  avec .

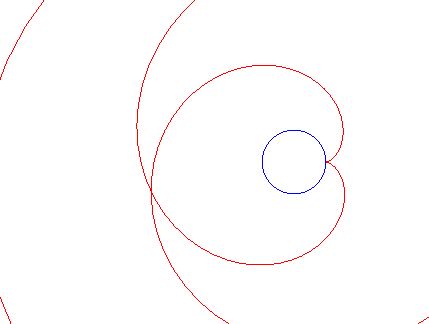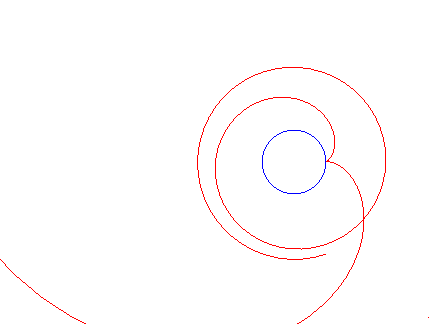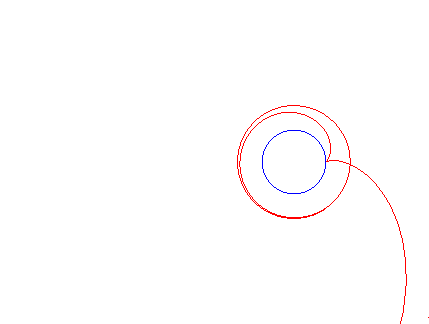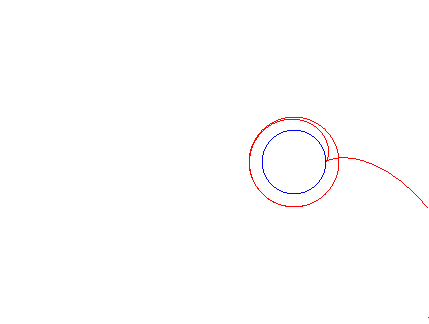
Animation pour diverses valeurs de k

 
 

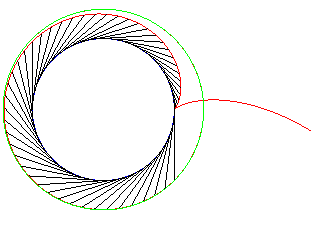
La branche pour est asymptote au cercle de rayon  (lequel fait partie de la développante oblique), et l'autre branche "se rapproche" d'une spirale logarithmique (l'une des spirales logarithmiques traversant avec un angle  les droites issues de O).	Exemple avec un angle de 45°
Pour  proche de 90°, la branche pour t > 0 commence avec des spires peu ou prou équidistantes, comme pour une spirale d'Archimède, puis les spires s'écartent, comme pour une spirale logarithmique.
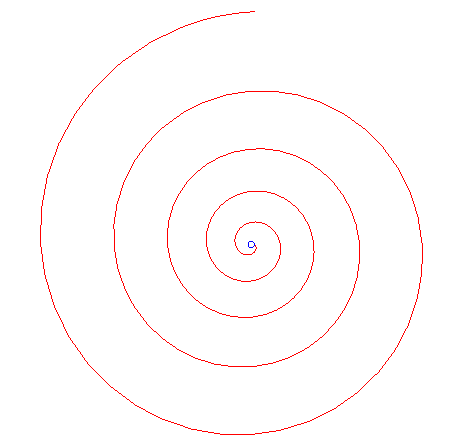Dans une figure de poursuites mutuelles avec des points de départ aux sommets d'un polygone régulier, les courbes sont des développantes obliques les unes des autres.
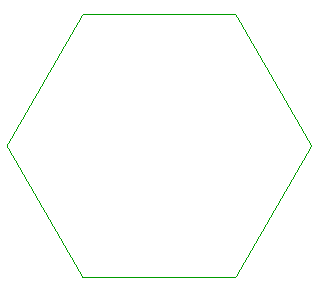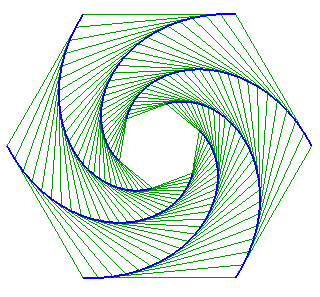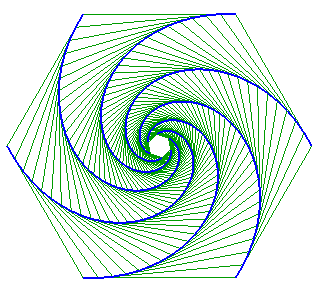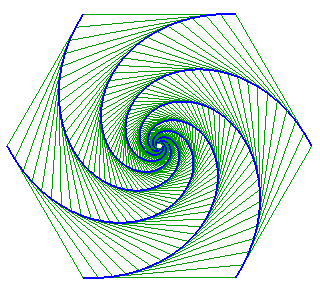On trouvera dans l'article ou le livre d'Apostol, une étude des développantes obliques des courbes cycloïdales. Ci-contre, exemple de la cardioïde.

 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2020