,
the current point M of an inverse evolutoid making an angle 
with the tangents is the locus of points 
where 
is defined by the differential equation: 
or 
(see
the notations).
Solution of this equation :
where 
. | next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
INVERSE EVOLUTOID OF A PLANE CURVE
| Notion studied in 1873 by abbé
Aoust (p. 119), in 2010 by Apostol
and Mamikon under the name of tanvolute.
Other names : oblique involute, generalized involute. |
| If M0 is
the current point of ,
the current point M of an inverse evolutoid making an angle
with the tangents is the locus of points
where
is defined by the differential equation:
or (see
the notations).
Solution of this equation :
where . |
The inverse evolutoids under an angle
of a plane curve are the curves of which
is the evolutoid of angle .
Those are
so the curves crossing
with an angle
the tangents to the curve .
For 
,
we find the involutes of .
EXAMPLE : INVERSE EVOLUTOID OF CERCLE
Cartezian paramétrization :
with  . |
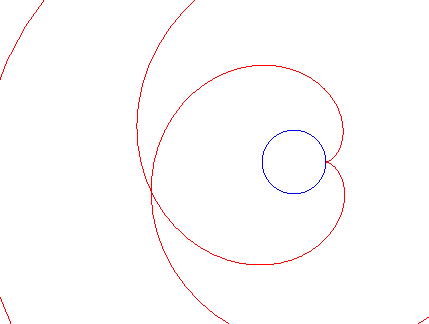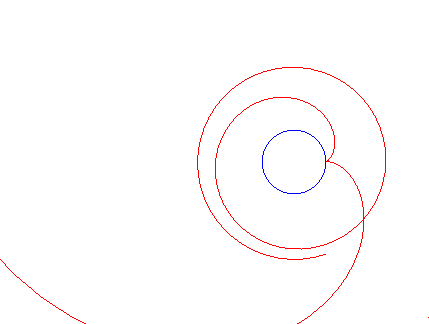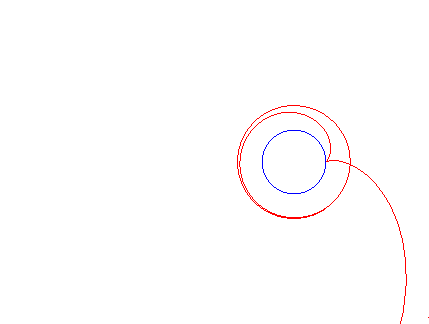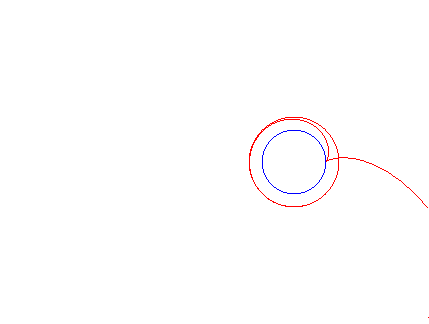
Animation for several values of k |
|
Oblique involute of a circle under an angle of 45 °. The curve has an asymptote branch to the circle
of radius |
 |
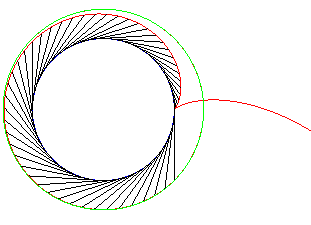| Pour proche de 90°, la branche pour t
> 0 commence avec des spires peu ou prou équidistantes, comme pour
une spirale d'Archimède, puis les spires s'écartent, comme
pour une spirale logarithmique.
For |
 |
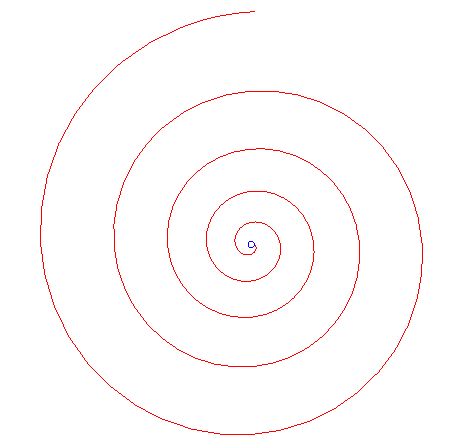| One will find in the article or the book of Apostol/Mamikon, a study on the oblique involutes of cycloidal curves. Opposite, example of the cardioid. |  |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2020
,
for 
,
and