Notion studied by Réaumur in 1709 and Lancret in 1811. bouasse 450, loria 297 See also this PhD thesis.

 

For an initial curve  with current point , the evolutoid is the set of points . Complex parametrization: . If the initial curve's intrinsic equation 2: , we get: Parametric intrinsic equation 1: . Intrinsic equation 2: .

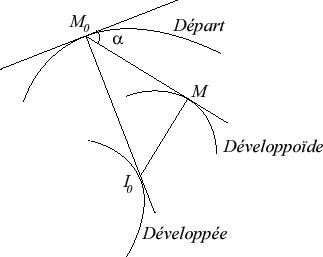
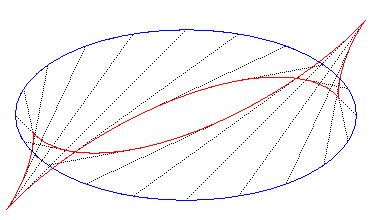
The evolutoids of a curve (G) are the envelopes of the lines (D) forming a constant angle a with the initial curve; when a = p/2, we get the evolute, and when a is 0 or 180°, we get the curve itself.
The characteristic point of the envelope can be constructed very simply by projecting the centre of curvature of the initial curve on the line (D) (Réaumur's theorem).

Examples:
    - the evolutoid of a line is the point at infinity of the varying line.
    - the evolutoids of a circle are concentric circles: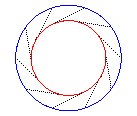 
    - the evolutoids of a logarithmic spiral are logarithmic spirals.
    - the evolutoids of a cycloidal curve (intrinsic equation ) are similar to the initial curve (intrinsic equation with ).
 

The evolutoids of the cycloid are isometric cycloids. Below, the evolutoid at 45°.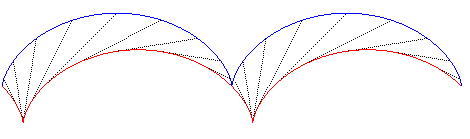

Below, the evolutoid at 60° of a cardioid.

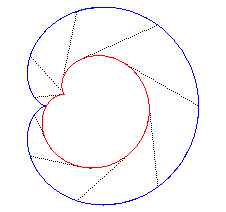next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017