| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ENVELOPE OF A FAMILY OF PLANE CURVES
| Notion studied by Leibnitz in 1694 and Taylor in 1715. |
If 
is defined by the Cartesian equation (1): f(x, y,
t)
= 0, the equation of the envelope is obtained by eliminating
t in
(1) and the equation (2):  (equivalent
to the visible outline
along Oz of the surface f(x,y,z) = 0).
If
is defined parametrically by (M(u,t))u,
the value of the parameter u as a function of t is obtained
by solving  . |
The envelope of a family of curves with one parameter
is the family 
of the characteristic points of the curves ,
limit points when t' goes to t of the intersection points
between
and 
; the
curve
is tangent, at any of its points, to a curve
and, "in general", any curve
is tangent at at least a point to ;
the restrictive cases are the following:
- on an interval, the curves
pass by one or several fixed points, in which case this point belongs to
the envelope.
- the curves do not intersect (for
example, concentric circles, or curves for which the intersection points
are imaginary).
With the notations above in the parametric case, since
the condition
is symmetrical with respect to u and t, the envelope of the
curves 
loci of the points (M(u,t))t
is the same as that of the curves ;
the envelope is in fact the locus of the points where a curve of the first
family is tangent to a curve of the second one. The two configurations
are said dual of one another.
 |
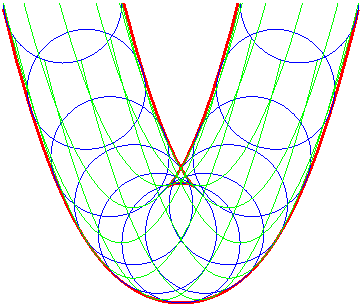Example: the envelope of a circle
with constant radius the centre of which describes a parabola is a curve
parallel
to the parabola.
We took M(t, u) = (t + cos u, t² + sin u) |
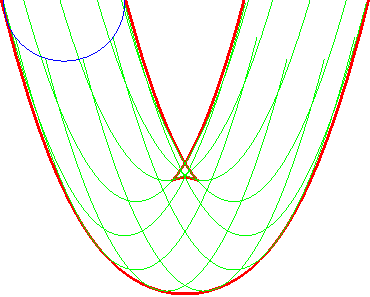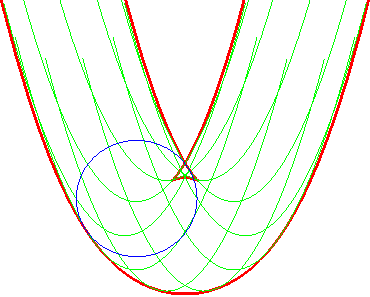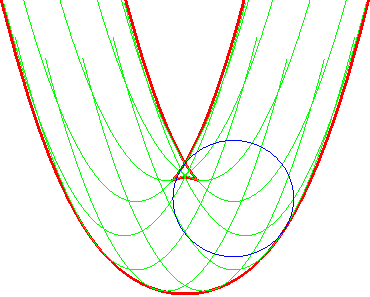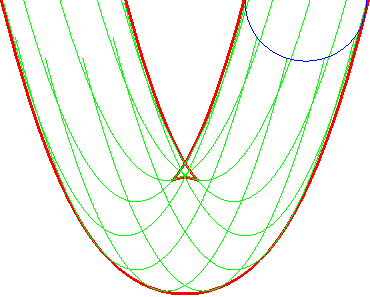
The envelope of the circles
... |
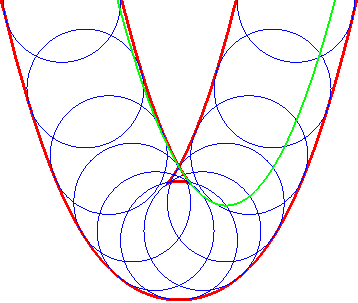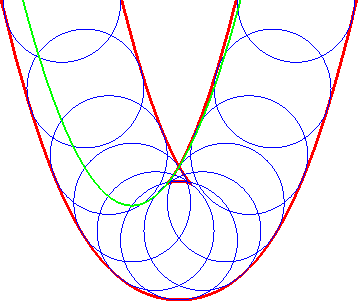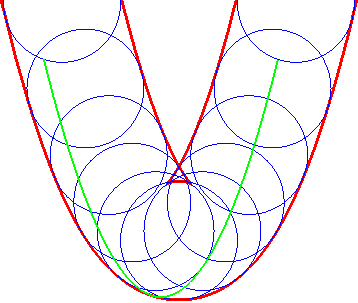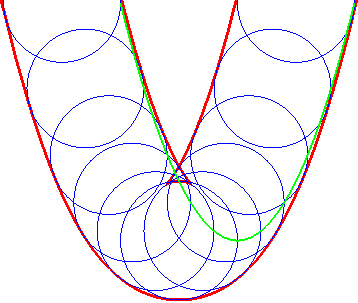
... is also that of the parabolas (G'u) |
| See also a nice example of duality at involute of a circle. |
The envelope can also be seen as the singular solution of the differential equation of which the curves (Gt) are solutions.
Special case: the envelope of a family of lines is a curve for which this family is the family of the tangents.
Envelopes of lines can be physically produced thanks to tables of wires.
Examples:
- Every curve is the envelope of its tangents,
or of its osculating circles.
- The evolute
of a curve is the envelope of the normals of the curve.
- The caustics
are the envelopes of rays reflected by an optical system.
- The curves parallel
to a curve are the envelopes of circles with constant radii centred on
this curve.
- The pedal
of a curve
with respect to a point O is the envelope of the circles with diameter
[OM] when M describes ,
and the orthotomic curve is
the envelope of the circles with centre M passing by O.
- The pedal
of a curve
with respect to a circle (C) is the envelope of the polar lines
with respect to (C) of the points on .
- An anallagmatic
curve is the envelope of the circles orthogonal to the inversion circle
and centred on the initial curve.
- The anticaustic
of a curve is the envelope of a circle centred on the curve and the radius
of which keeps a constant ratio with the distance between the centre of
the circle and a fixed point.
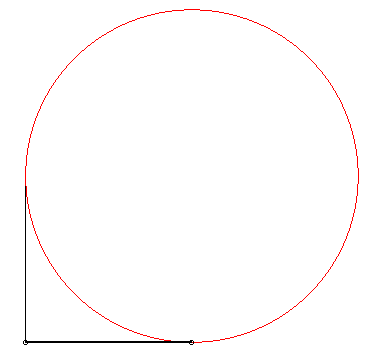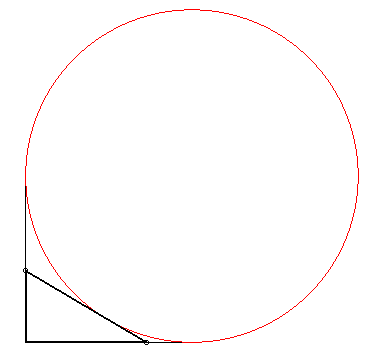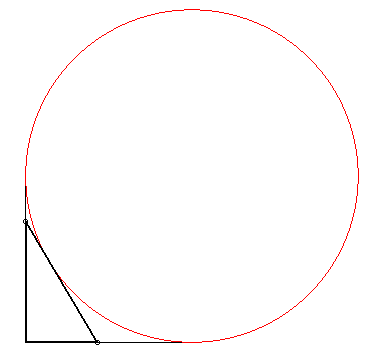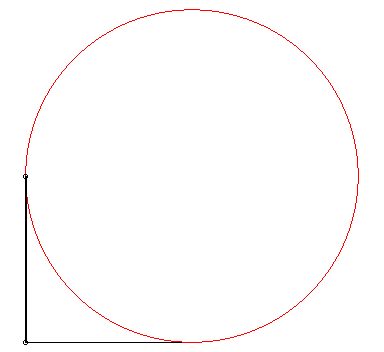
| - The envelope of a line (AB) when A and
B
move along the axes Ox and Oy is
- an astroid: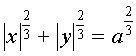 
when the length AB is a constant equal to a (see, more generally,
the Cremona generation of epi-
and hypocycloids)
- the reunion of four arcs of parabola 
when OA + OB is a constant equal to a (see at Lamé
curve)
- the reunion of four arcs of circle with radius a :  when
the perimeter of the triangle OAB is a constant equal to 2a,
- the reunion of two rectangular hyperbolas: 
when the area of the triangle OAB is a constant equal to  . |
 |
- In the movement of a plane over a fixed plane, it is often interesting to consider the envelope in the fixed plane of a line in the moving plane.
- The shooting parabola is the envelope of all the trajectories of shots taken at a given point with a constant initial speed.
See also the envelopes
of surfaces and the envelopes
of 3D curves.
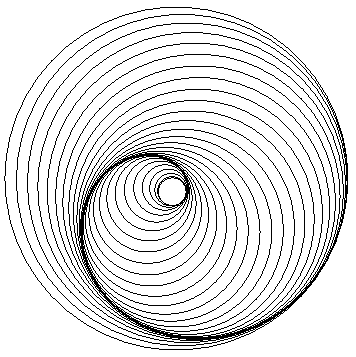
| Set of the osculating circles of an Archimedean spiral.
There is no need to trace the envelope... |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2023