Parallel curves

PARALLEL CURVE OF A CURVE

Notion studied by Leibniz in 1692.

The curves and are parallel if respective current points M₁ and M₂ can be determined so that .
For an initial curve with current point , a parallel curve is a set of points .
Cartesian parametrization: .
The parallel curves of an algebraic curve are algebraic.
Curvilinear abscissa at the current point on 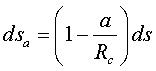(oriented by the same tangent vector as ): .
Radius of curvature: .
The length of an arc of is equal to the length of the corresponding arc on minus a multiplied by the angle spanned by the tangent between the beginning and the end. For example, for an eight-like curve, the two curves have the same length. The length of is equal to the mean of the lengths of and .
The area of the strip included between two corresponding arcs of and is equal to the length of the median arc of times a, under the condition that the strip does not intersect itself, nor does it overlap on the evolute of .

Two curves are said to be parallel of one another if any curve normal to one is normal to the other; it can be proved that, then, the distance between two points with common normal is a constant, called parallelism distance. Do not mistake with the image of a curve under a translation.

Two curves are therefore parallel to one another if they are the loci of the ends of a segment line of constant length moving perpendicularly to its direction, which is equivalent to saying that the line carrying this segment rolls without slipping on its envelope.

See also at reptoria the generalisation of parallel curves by the crawling motion of a circle on a curve.

As well as for lines, the parallelism relation of plane curves is an equivalence relation.
An equivalence class is the set of all trajectories of points linked to a line rolling without slipping on a curve ; the moving line is the common normal line to all the parallel curves, and the fixed line is the common evolute to all these curves.
The parallel curves of a curve are therefore the involutes of its evolute.

The involute presenting (in general) a cusp at a point of the starting curve, the evolute appears as the place of the cusp points of the parallel curves.
Opposite, animation of a normal line rolling without slipping on the evolute, drawing a parallel with cusp (in red), which is one of the involutes of the evolute (in green).

The parallel curves of a curve are the curves , parallel of index a of , obtained by algebraically copying a "length" a from the points on on the oriented normal; in other words, they are the loci of the points M = where is the normal vector at M₀. Since the parallelism relation is symmetrical, is also parallel to .

The reunion of and (G_-a) is the envelope of the circles with radius a centred on ; therefore, it is also the visible outline of a tube, the bore of which is projected along .

If the curve is placed on a plane in a motion of circular translation with radius a with respect to a fixed plane, then the envelope in the fixed plane is, again, the reunion of and .

The parallel curves of a curve can also be considered as the plane contour lines of an equal slope surface with directrix .

Physical interpretation: if the curve is a light source, according to the Huygens principle, the "wavefronts" are the envelopes of the elementary circular wavelets emitted by all the points on the curve ; they are therefore exactly the curves parallel to .

The singularities of parallel curves describing the evolute of the initial curve, with the previous physical interpretation, the evolute therefore represents the place where the light rays emitted by the curve are concentrated.

Examples:
    - the curves parallel to a line are the lines parallel to this line (!)
    - the involutes of a curve are parallel to one another.
    - the toroids are the parallel curves of the ellipse
    - the Cayley sextic is one of the parallel curves of the nephroid
    - The parallel curves of the parabola x² = 2p y are the curves parametrized by:

Opposite illustration of the construction of the two parallels at given distance to the parabola, by envelope of a circle whose center describes the parabola (not plotted in the figures), or by envelope of "circular translated"of the parabola.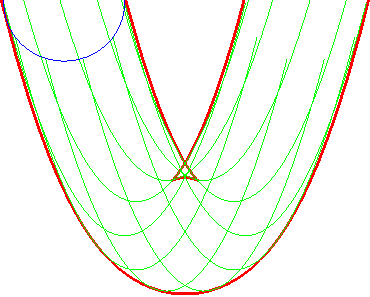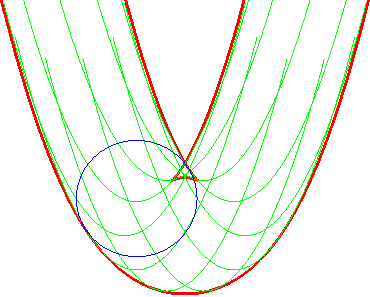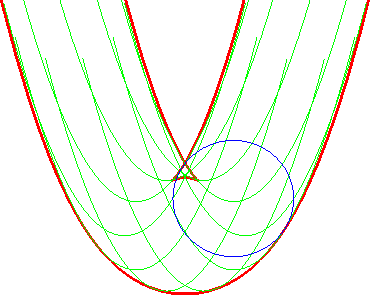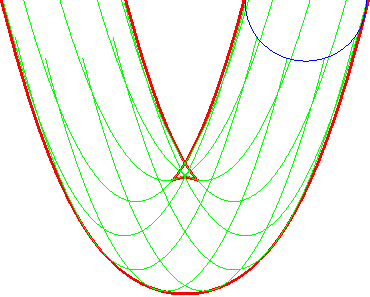

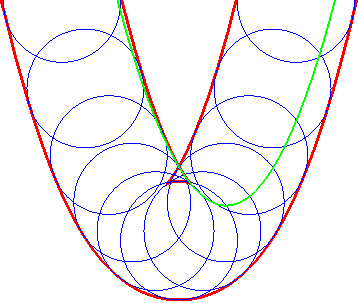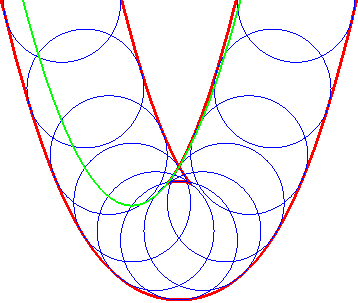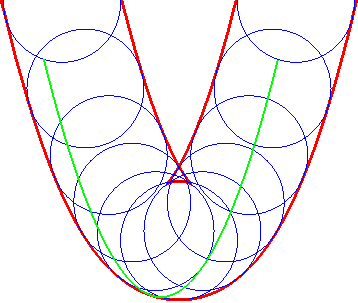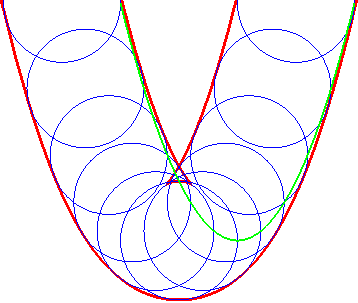- It can happen that the curves and are equal. Then, the curve is parallel to itself at distance 2a.

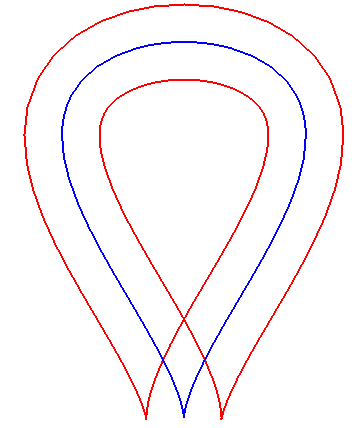The red curve is parallel in two ways to the blue curve, and self-parallel.

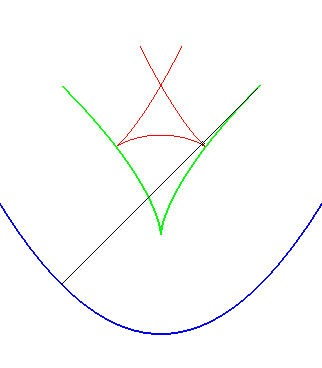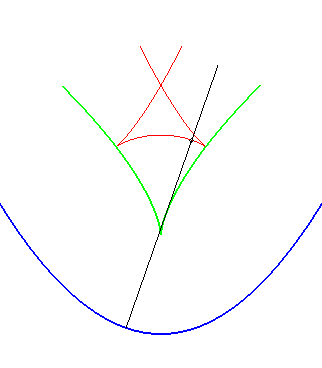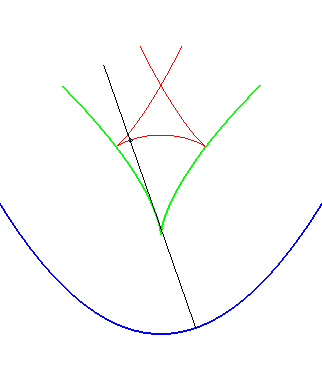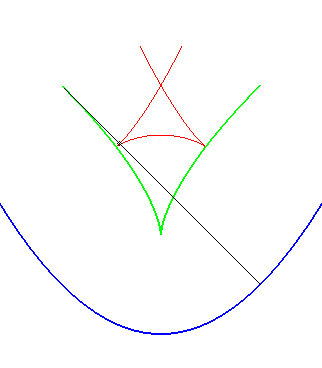
A similar notion is the notion of contour line of the function "distance (of a point on the plane) to the curve", called distance curve (or line). These contour lines are composed of portions of parallel curves and arcs of circles, and are interesting because they form a partition of the plane, as opposed to parallel curves.

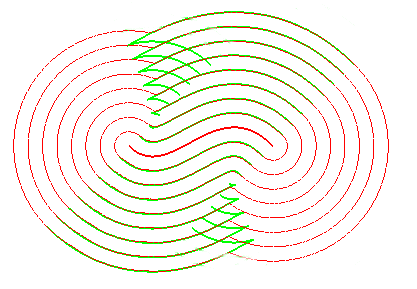
In green, the parallel curves, and in red, the contour lines of the function "distance to the curve"; when they do not coincide, the latter are composed of arcs of circles.