If M0 is the current point on , the current point M of an involute is the locus of the points , which yields: Cartesian parametrization: . Complex parametrization: . Radius of curvature: .

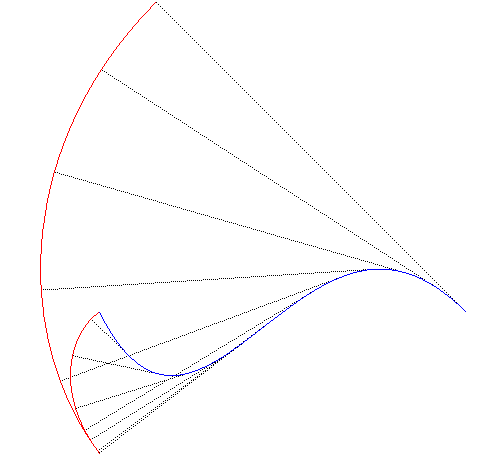
The involutes of a plane curve  are the curves traced by the end of a wire tightened along  and winding itself along . In other words, they are the traces on the plane of a point on a line pivoting without slipping on  (therefore, they are special cases of roulettes).

Thus, they also are the orthogonal trajectories of the family of the tangents to the curve, or also the curves for which the initial curve is the evolute.

The involutes of a curve are parallel to one another.
 
 

It will be noticed (cf. figures) that an inflexion point on the initial curve yields a cuspidal point of the second kind on the involute, as the Marquis de l'Hospital had already understood in 1696 (see this text).

 

Examples: (see also at evolute)
 

initial curve	origin	involute, or one of them
circle	any point	involute of a circle!
point	any point	circle
cycloid	vertex	the same cycloid, translated
cardioid	vertex	similar cardioid with ratio 3
nephroid	vertex	similar nephroid with ratio 2
nephroid	cuspidal point	Cayley sextic
epicycloid with parameter q	vertex	similar epicycloid with ratio (q + 2)/q
deltoid	vertex	similar deltoid with ratio 1/3
astroid	vertex	similar astroid with ratio 1/2, Maltese cross
hypocycloid with parameter q	vertex	similar hypocycloid with ratio (q-2)/q
logarithmic spiral	centre	logarithmic spiral
catenary	vertex	tractrix
logarithmic	any point	involute of an exponential
involute of a circle	cuspidal point	Norwich spiral

See the generalisation to 3D curves.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017