TOROID

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TOROID









| Curve studied by Cauchy in 1841, Catalan and Breton des
Champs (who named it) in 1844.
The name toroid comes from torus. |
| Cartesian parametrization: for the ellipse: Biquartic. |
The toroids are the parallel
curves of the ellipse, hence the
involutes
of the evolute of the ellipse.
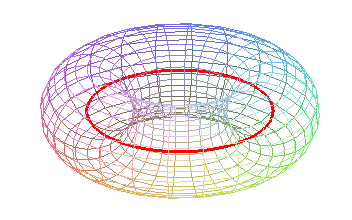
The name comes from the fact that the toroids are none
other than the visible
outlines of the torus.
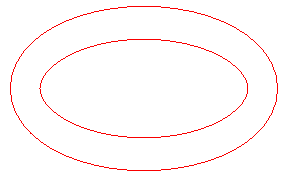
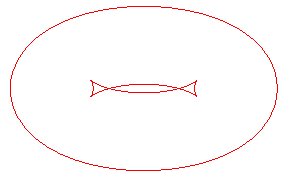
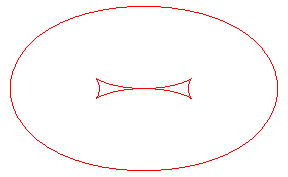
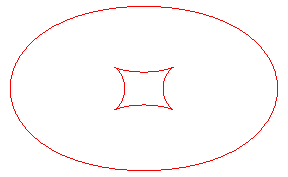
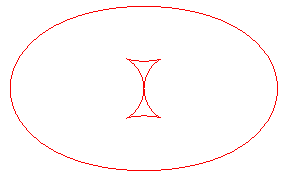
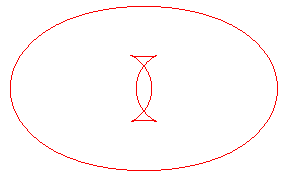
| The toroids are, in general, composed of two ovals, except
when the distance is the distance between the extrema of the radius of
curvature of the ellipse Opposite, evolution of the toroid, as the distance d to the ellipse increases. In green, the evolute of the ellipse. |
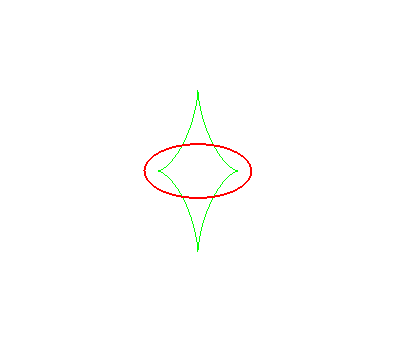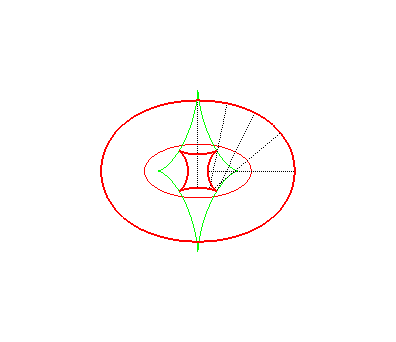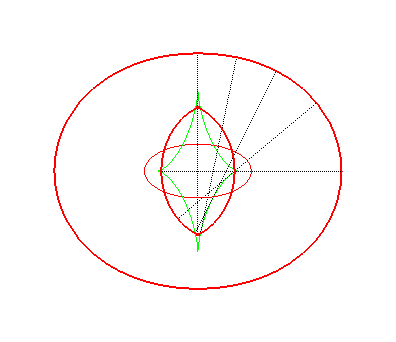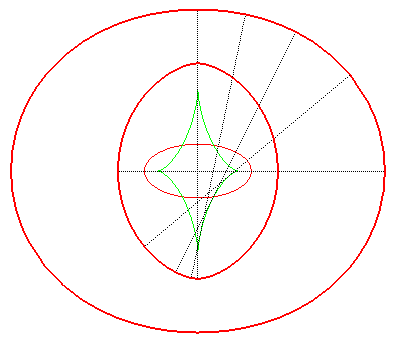 |
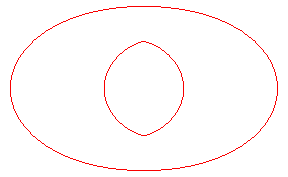
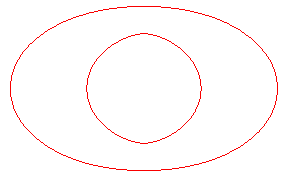
| Opposite, the toroid (in green) of the blue ellipse,
in the case d = 2a, length that also is the diameter of the
ellipse.
With the curve traced in red, we get a curve with the same diameter as the ellipse and which is a curve with constant width, looking like the Reulaux triangle, and different from the obvious circumscribed circle of the ellipse. |
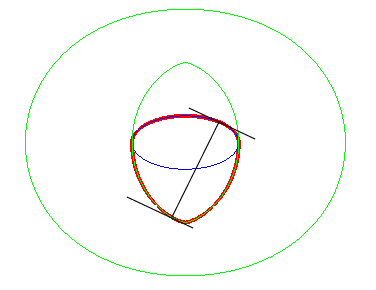 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017