next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

VISIBLE OUTLINE OF A SURFACE


 
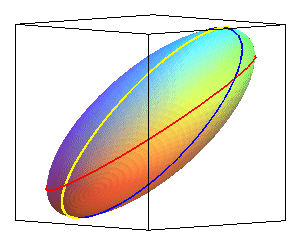
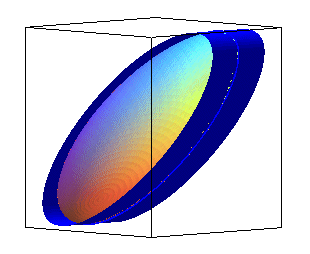
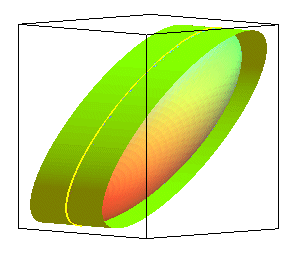
View of an ellipsoid and 3 of its visible outlines, for observers located at infinity in the directions Ox, Oy, Oz and the corresponding contact cylinders.
 

 
Given a direction D, we call visible outline of a surface (S), in this direction and for an observer at infinity, the locus of the projections on a plane P perpendicular to D of the points on the surface for which the tangent plane is parallel to D.

Therefore, the visible outline is also:
    - the intersection between P and the contact cylinder of the surface in the direction D, composed of the lines parallel to D and tangent to (S);
    - the envelope of the sections between P and the tangent planes parallel to D;
    - the envelope of the projections on P of the contour lines of the surface, associated to the direction D;
    - more generally, the envelope of the projections on P of any family of curves generating the surface.

Certain authors refer to the locus, on the surface, of the points for which the tangent plane is parallel to D as the visible outline; we will refer to it as the real visible outline, the other one being the projected one.

 Given a direction D, we call visible outline of a surface (S), in this direction and for an observer located at A, the locus of the projections with centre A on a plane P, perpendicular to D and not containing A, of the points on the surface for which the tangent plane passes by A.

Therefore, the visible outline is also:
    - the intersection between P and the contact cone of the surface with centre A, composed of the lines passing through A and tangent to (S);
    - the envelope of the sections between P and the tangent planes passing by A;
    - the envelope of the conic projections with centre A on P of any family of curves generating the surface.
Note that the visible outline remains similar to itself when P varies.
Certain authors refer to the locus, on the surface, of the points for which the tangent plane passes by A as the visible outline; we will refer to it as the real visible outline, the other one being the projected one.

 
Visible outline in the direction Oz for an observer located at infinity:
if the surface is defined by the Cartesian equation (1): f(x,y,z)=0, then the equation of the outline is obtained by eliminating z from (1) and (2): .
If the curve has a parametric definition as (M(u,v)), we get v = v(u) by writing  and the parametrization of the visible outline is x = x(u,v(u)), y = y(u,v(u)).		 Visible outline in the direction Oz for an observer located at A(0,0,a):
if the surface is defined by the Cartesian equation (1): f(X,Y,Z)=0, then the equation of the outline in the plane xOy is obtained by eliminating X, Y and Z from (1), (2):  and (3): .
If the curve has a parametric definition as (M(u,v)), we get v = v(u) by writing , and the parametrization of the visible outline is x = x(u,v(u)), y = y(u,v(u)).

Examples:

    - the visible outlines of a sphere are circles (and, conversely, a surface for which all the visible outlines for an observer at infinity are circles is a sphere);
    - the visible outlines (real or projected, at finite distance or not) of a quadric are conics (therefore, they are planar);
    - the visible outlines of an algebraic surface of degree n are algebraic surfaces of degree n(n - 1) (?);
    - the projected visible outline of a tubular surface is composed of two curves parallel to the projection on xOy of the central curve. In particular, the visible outlines of the torus are the curves parallel to the ellipse, hence their name of toroids.
    - the contact cylinder in the direction D (resp. with centre A) of a developable surface is composed of the planes tangent to the surface and parallel to D (resp. passing by A); the real visible outline is composed of the directrices for which the tangent plane is parallel to D (resp. passing by A), and the projected visible outline is composed of straight lines (two lines for a cone or a cylinder of revolution).
 
 
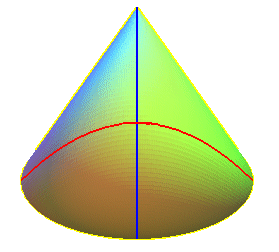
Opposite, view of a surface and its visible outlines for an observer located at finite distance, the real one in blue, the projected one in black, with, on the right, the contact cone.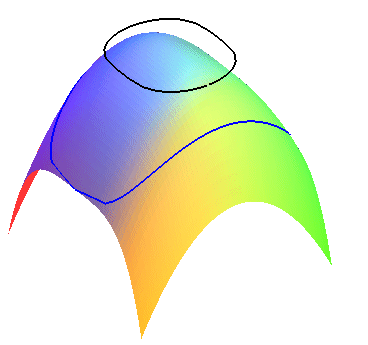

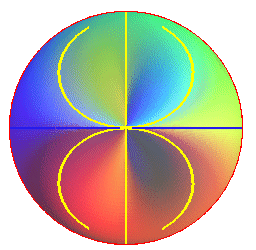
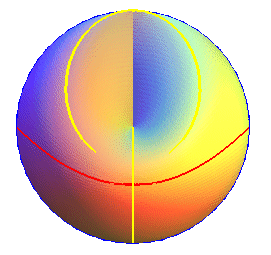
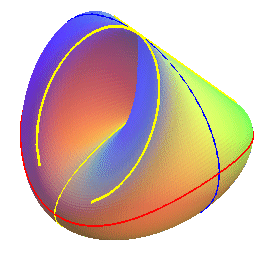
Below, views of the cross-cap with three visible outlines for observers located at infinity in the direction Oz (in red), Ox (in blue), and Oy (in yellow).
 
 
 

 

The intersection of three cylinders with perpendicular axes has three visible outlines at infinity in these three directions. They are circles with same radii, but the intersection is not a sphere.
Image: Alain Esculier.

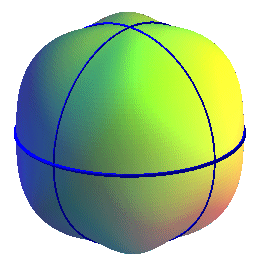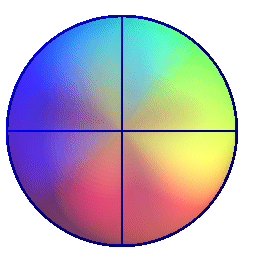This blistered sphere, whose spherical equation is  has the same property, while having a tangent plane at every point.

A similar notion is defined in topology: the visible outline of a set X of the space is the boundary of the projection of X on a plane P. The projection is orthogonal for an observer at infinity, and has a centre A for an observer at A. The two notions coincide for example when X is a surface of class C1, boundary of a convex set of the space.
 
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL 2019