BONNET CROISÉ
Cross-cap,
Kreuzhaube
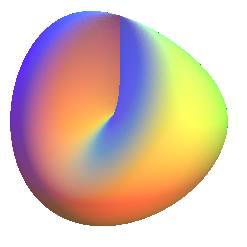
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
BONNET CROISÉ
Cross-cap,
Kreuzhaube
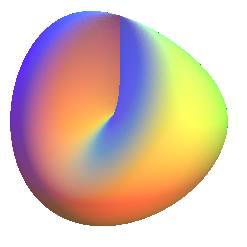
| Surface étudiée par Steiner ???
Autre nom : mitre. |
Paramétrisation cartésienne n°1 : 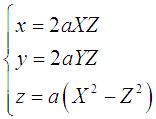 avec
avec Paramétrisation cartésienne n°2 : Paramétrisation cartésienne n°3 : Paramétrisation cartésienne n°4 : |
Le bonnet croisé est l'image de la sphère
quotientée par la relation d'antipodie (autrement dit, le plan
projectif réel), par l'application : .
| Le bonnet croisé est l'une des plus simples immersions
du plan projectif réel
dans Il ne possède qu'un segment d'auto-intersection terminé par deux points cuspidaux (ici O et (0, 0, a)) (comparer avec la surface romaine et la surface de Boy, qui sont deux autres immersions du plan projectif). |
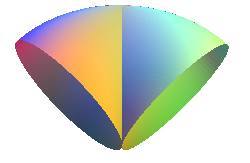 |
| La figure ci-contre illustre le fait que le bonnet croisé est un modèle du plan projectif : |
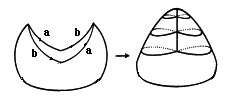 On part d'une sphère trouée (homéomorphe au disque), et on plaque bord à bord a avec a, et b avec b, pour former le segment d'auto-intersection |
| Autre construction, à partir d'un disque au bord tordu en un huit, ayant déjà une auto-intersection. |
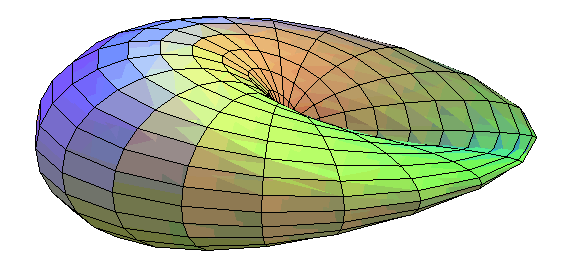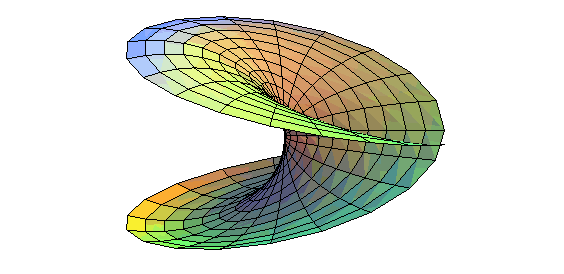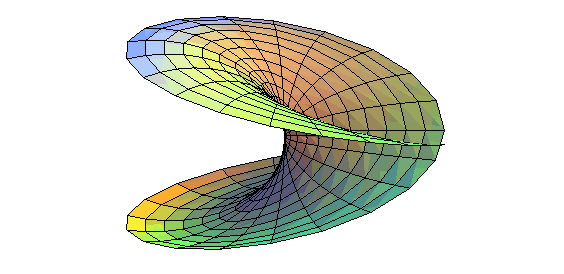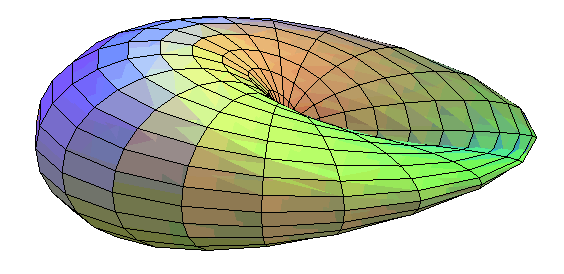 |
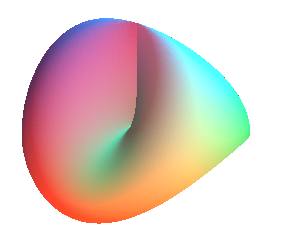 .
C'est alors vraiment un bonnet au sens physique, mais d'un point de vue
topologique, c'est un ruban de Möbius.
.
C'est alors vraiment un bonnet au sens physique, mais d'un point de vue
topologique, c'est un ruban de Möbius.
Le bonnet croisé possède aussi d'intéressantes propriétés géométriques. Il est en particulier de 3 façons différentes réunion d'une famille d'ellipses :
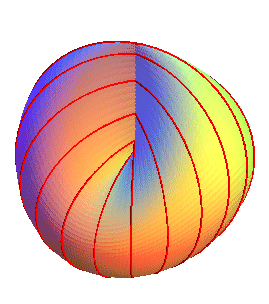
| Première famille (cf. paramétrisation
n°2) : les sections par les plans contenant
Oz
d'angle
polaire
q sont les ellipses, de
sommets secondaires (0, 0, a) et |
 |
||
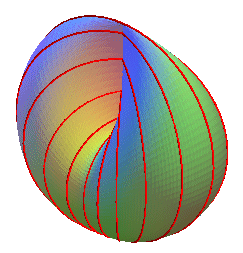
| Si l'on remplace les ellipses précédentes
par des cercles, on obtient une surface cerclée
de paramétrisation cylindrique : Cette dernière surface, homéomorphe à la précédente, est image par inversion du conoïde de Plücker d'ordre 1, les droites du conoïde devenant les cercles de ce bonnet croisé. |
 |
||
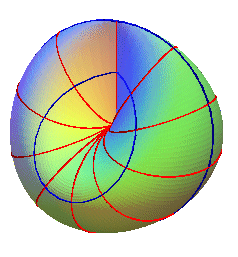
| Deuxième famille (cf. paramétrisation
n°3) : les sections par les plans contenant
Oy En bleu le lieu des sommets. |
 |
||
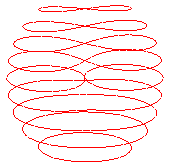
| Troisième famille (cf. paramétrisation
n°4) : les sections par les plans |
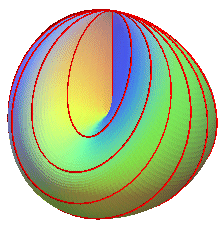 |
||
|
 |
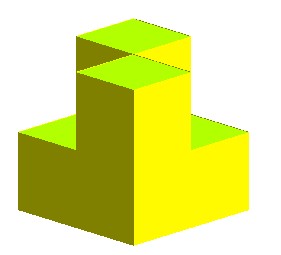
| Voici une version polyédrique du bonnet croisé.
Attention, ce n'est pas un vrai polyèdre : l'arête double centrale est commune à 4 faces. |
  |
Il ne faut pas confondre le bonnet croisé avec le pseudo-bonnet croisé :

| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014