SURFACE ROMAINE
Roman
surface, römische Fläche
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE ROMAINE
Roman
surface, römische Fläche


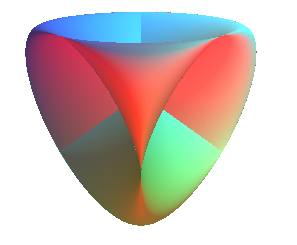
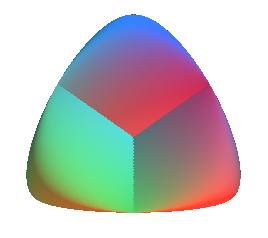
| Surface étudiée par Steiner
en 1844.
Cette surface a été ainsi nommée par Steiner car il l'a découverte lors d'un séjour à Rome. |
| Équation cartésienne comme surface
tétraédrique de Kümmer : de sorte que f = 0 est l'équation de la sphère de centre O et de rayon a et pqrs = 0 l'équation d'un tétraèdre régulier centré en O et dont les arêtes sont à distance a de O. Équation cartésienne dans un repère tourné de 45° autour de Oz : Paramétrisation cartésienne : soit, en faisant Soit, encore, en faisant maintenant Surface quartique unilatère, cas particulier de surface de Steiner. |
La surface romaine est l'image de la sphère
(centre
O, rayon 1) quotientée par la relation
d'antipodie (autrement dit le plan
projectif réel) par l'application : .
C'est historiquement la première représentation
du plan projectif réel comme surface de .
Elle possède trois segments d'auto-intersection formant un trièdre
trirectangle terminés chacun par deux points
cuspidaux et se coupant en leur centre en un point triple (ici O).
La définition ci-dessus comme cas particulier de
surface
de Kummer montre qu'elle possède les symétries du tétraèdre
régulier.
Avec la deuxième équation les sommets du
tétraèdre sont les points ,
avec un nombre pair de signes -.
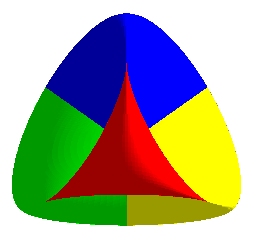
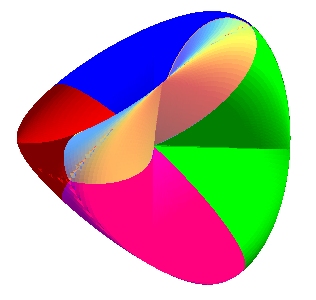
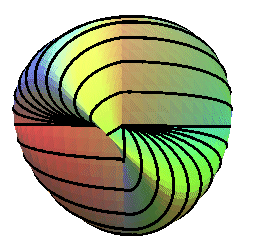
| La surface romaine est de 3 façons réunion
d'ellipses (avec la seconde équation ci-dessus, ce sont les sections
par les plans contenant les axes) ; on pourrait dire que la surface romaine,
à l'instar du bonnet
croisé, est une surface triplement "ellipsée".
Ci-contre est représentée la famille d'ellipses situées dans les plans passant par la ligne double verticale. |
 |
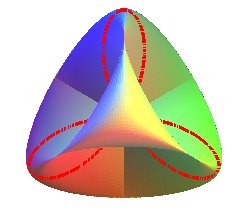
| Les sections par les plans perpendiculaires aux axes
de rotation d'ordre 3 forme la famille des hypotrochoïdes
à trois branches.
En particulier, la section par le plan central est le trifolium régulier. |
 |
| Les sections par les plans perpendiculaires aux lignes doubles sont les lemniscates de Booth. | 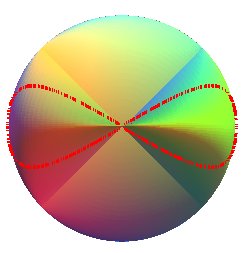 |
| Voici enfin une version polyédrique de la surface romaine : | et une autre, où les cubes ont été tronqués en des tétraèdres orthocentriques : |
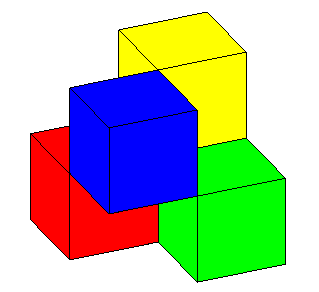 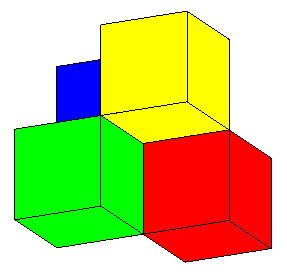
Retrouvez bien les les 3 segments doubles terminés par les 6 points de pincement, les 4 sommets et le point triple ! |
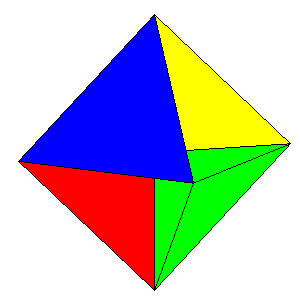 |
| Attention 1 : si vous voyez les cubes en creux, vous êtes victime
d'une illusion !
Attention 2 : ce n'est pas un vrai polyèdre : les arêtes doubles sont communes à 4 faces |
Là également, ce n'est pas non plus un polyèdre, mais si l'on réunit les faces centrales en 4 carrés, on obtient un polyèdre croisé, semi-régulier de surcroit, appelé tétrahémihexaèdre. |
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014