Hypotrochoïde

HYPOTROCHOÏDE
Hypotrochoid, Hypotrochoide

hypocycloïde raccourcie avec q = 7/3 hypocycloïde allongée avec q = 7/3

Du grec hupo "au-dessous" et trokhos "roue".
Autre nom : hypocycloïde allongée ou racourcie.
Pour tracer des hypotrochoïdes : aesculier.fr/fichiersMaple/cycloide/epihypocycloides.html

Paramétrisation complexe : , soit où a est le rayon du cercle de base, b = a / q celui du cercle roulant et d = k b la distance du point au centre du cercle mobile (q > 1).
Paramétrisation cartésienne : .
Paramétrisation polaire : .

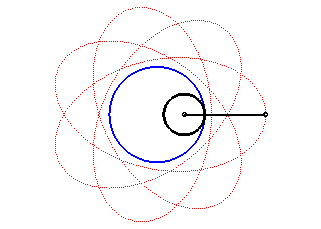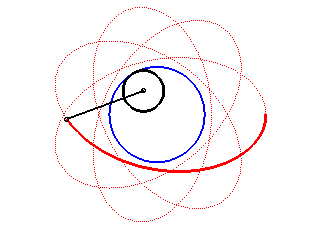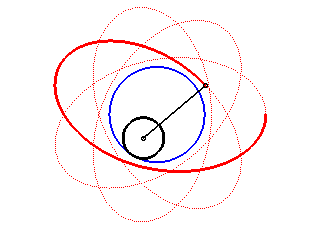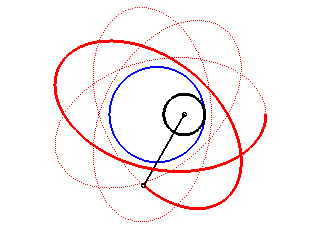
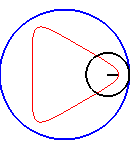
Les hypotrochoïdes sont les courbes décrites par un point lié à un cercle (C) roulant sans glisser sur et intérieurement à un cercle de base (C₀) ; ce sont donc les courbes que l'on obtient avec un spirographe avec disque interne.

Autre façon de dire la même chose : les hypotrochoïdes sont les roulettes d'un mouvement plan sur plan dont la base est un cercle et la roulante un cercle intérieur au premier.

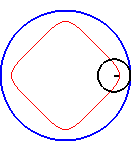
Pour d = b, soit k = 1, on obtient les hypocycloïdes.

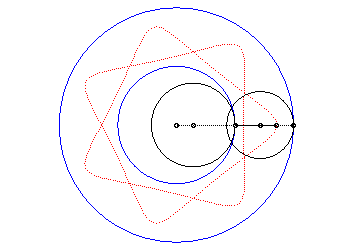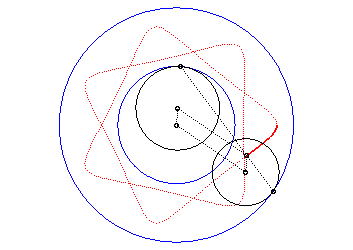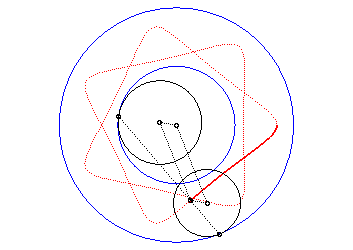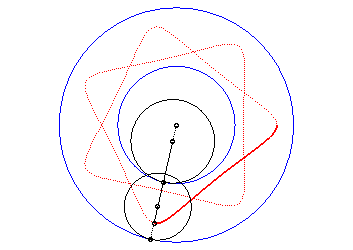Si l’on remplace a par , b par et d par a – b, l’hypotrochoïde obtenue est identique à celle de départ (propriété de double génération de l’hypotrochoïde).

On en déduit que si l’on conserve a, mais change q en et k en , l’hypotrochoïde obtenue est homothétique de celle de départ dans le rapport k. On obtient donc toutes les hypotrochoïdes en ne considérant que le cas .

Pour q = 2, on obtient les ellipses : .
Le mouvement plan sur plan correspondant est aussi obtenu par glissement.

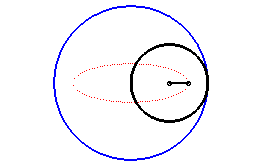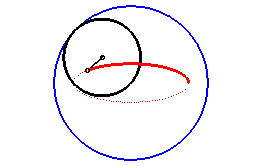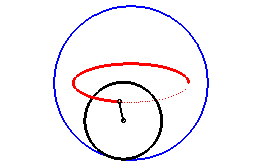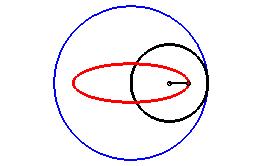Pour q > 2, la courbe s'appelle aussi hypocycloïde raccourcie si k < 1, hypocycloïde allongée si k > 1.

Attention, d’après ce qui précède, dans le cas 1 < q < 2, les hypocycloïdes raccourcies sont obtenues paradoxalement pour k > 1 et les hypocycloïdes allongées, pour k < 1 !

Voici les différentes formes en fonction des valeurs de k.

Il est remarquable que pour , l'hypocycloïde raccourcie tourne constament sa concavité vers le centre (ci-contre, cas q = 3, k = 1/2 – 1/10).
Notons que pour la trochoïde rectiligne, il y a toujours des changements de concavité.

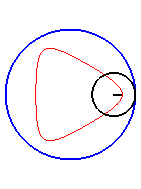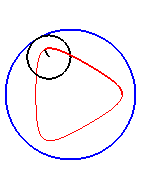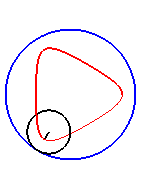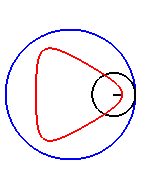Le cas limite est ; il y a alors un méplat.

Pour , la courbe ondule, avec des points d'inflexion.

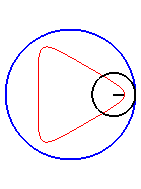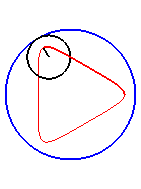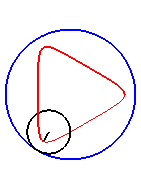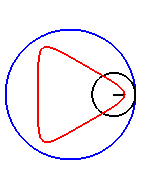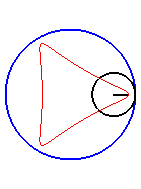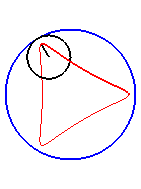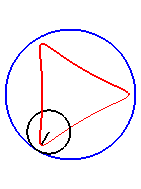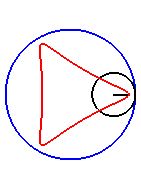Pour k = 1, on obtient l'hypocycloïde, avec des points de rebroussements.

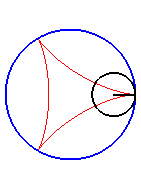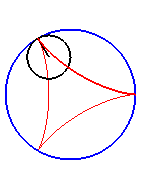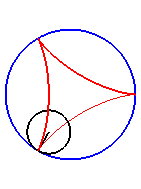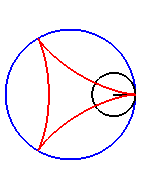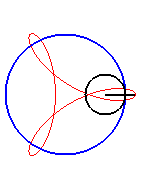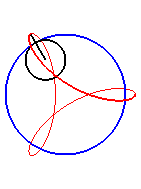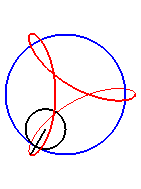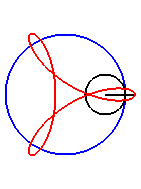Pour, la courbe fait des boucles, avec des portions concaves et convexes, (vitesse angulaire positive, puis négative alternativement)

Pour k = q – 1 (soit d = a – b)), on obtient une rosace d'indice n > 1 , d'équation polaire :

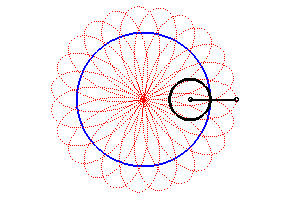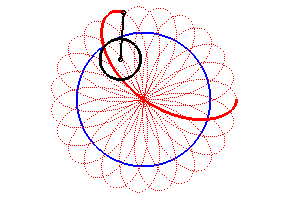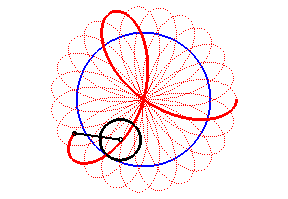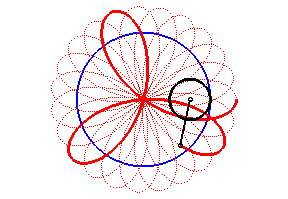Pour k > q – 1, la courbe est de nouveau convexe.

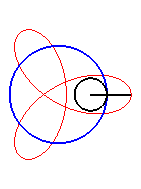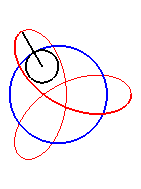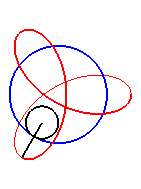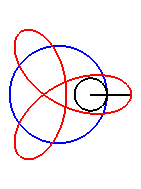On peut aussi définir les hypotrochoïdes comme les trajectoires d’un mouvement qui est composé de deux mouvements circulaires de sens contraires, de paramétrisation complexe : () ; ce sont des hypocycloïdes si , des ellipses si , des hypocycloïdes allongées si et ou et , des hypocycloïdes raccourcies si et ou et (on peut alors prendre , , d = r₂, donc ).
Le premier bras a une vitesse angulaire (par rapport au plan fixe) quadruple de celle du deuxième : on obtient une hypotrochoïde de paramètre q = 4 + 1 = 5.

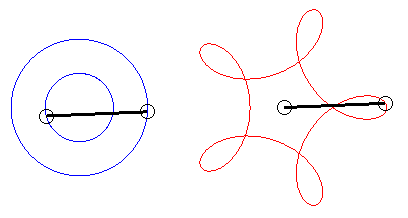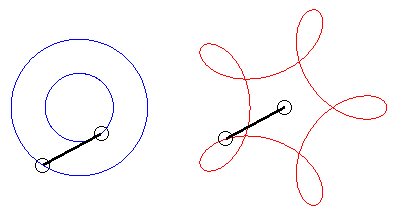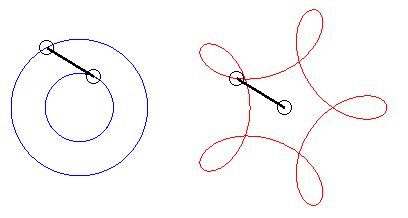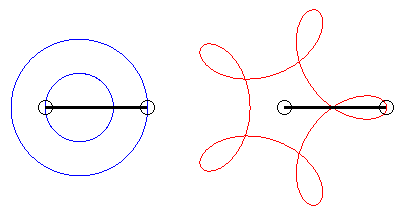L'écriture donne l'interprétation suivante des hypotrochoïdes : si deux corps sont en rotation uniforme et de sens contraire dans un plan fixe, la trajectoire apparente de l'un dans un plan lié au deuxième et en translation par rapport au plan fixe est une hypotrochoïde.

Forme des courbes dans différents cas :

Valeur de q Valeur de

3 2
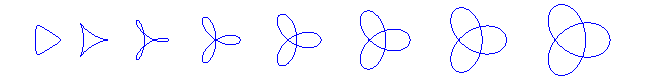
(voir la surface romaine)

4 3

5 4

5/2 3/2

7/2 5/2

7/3 4/3

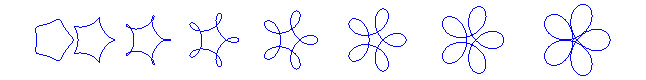L'hypotrochoïde de paramètre q = n/m constitue une approximation "arrondie" du polygone régulier de type (n, m) ; pour que les portions entre deux sommets soient le plus rectiligne possible on peut prendre le cas limite où cette portion de possède pas de points d'inflexion, qui correspond au cas k = 1 / (q –
1) ; ci-contre quelques vues correspondant à ce cas.
Pour q = 4, ce phénomène est utilisé dans le mécanisme des montres carrées.
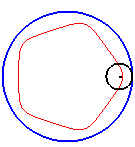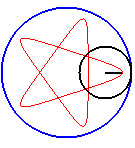
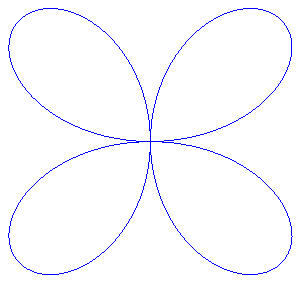
Des hypotrochoïdes en triangle, carré, pentagone et pentagone étoilé (q =3, 4, 5, 5/2)

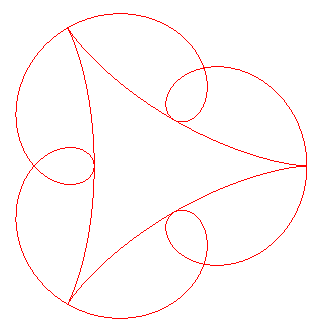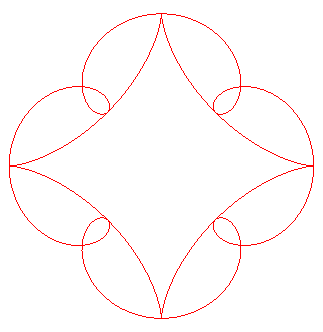Etant donné une hypocycloïde de paramètre , il existe une hypotrochoïde circonscrite, de paramètre , avec et .

Les hypotrochoïdes et les épitrochoïdes constituent les trochoïdes à centre.

Les hypotrochoïdes sont aussi des projections planes des courbes de Caparéda, ou courbes des satellites.

Voir la généralisation aux polytrochoïdes à la page sur les trochoïdes à centre.

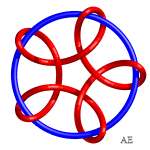
Voici diverses hypotrochoïdes passées en 3D et nouées :

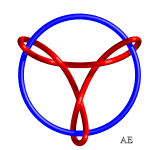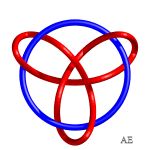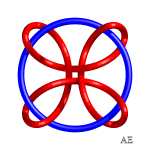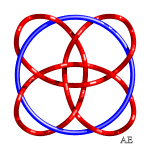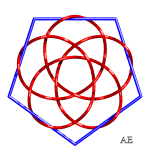Entrelacs 9.2.24 Entrelacs 9.2.40 Voir cette page

Courroie d'engrenage mise en forme d'hypotrochoïde par Lévi Capareda pendant un cours de sciences industrielles... q = 4, k = 3 q = 4, k = 8

Gravure de J. Mandonnet

Dessins de spirographe
Un spirographe marin !

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Il est remarquable que pour , l'hypocycloïde raccourcie tourne constament sa concavité vers le centre (ci-contre, cas q = 3, k = 1/2 – 1/10). Notons que pour la trochoïde rectiligne, il y a toujours des changements de concavité.
Le cas limite est ; il y a alors un méplat.
Pour , la courbe ondule, avec des points d'inflexion.
Pour k = 1, on obtient l'hypocycloïde, avec des points de rebroussements.
Pour, la courbe fait des boucles, avec des portions concaves et convexes, (vitesse angulaire positive, puis négative alternativement)
Pour k = q – 1 (soit d = a – b)), on obtient une rosace d'indice n > 1 , d'équation polaire :
Pour k > q – 1, la courbe est de nouveau convexe.

On peut aussi définir les hypotrochoïdes comme les trajectoires d’un mouvement qui est composé de deux mouvements circulaires de sens contraires, de paramétrisation complexe : () ; ce sont des hypocycloïdes si , des ellipses si , des hypocycloïdes allongées si et ou et , des hypocycloïdes raccourcies si et ou et (on peut alors prendre , , d = r₂, donc ).	Le premier bras a une vitesse angulaire (par rapport au plan fixe) quadruple de celle du deuxième : on obtient une hypotrochoïde de paramètre q = 4 + 1 = 5.
L'écriture donne l'interprétation suivante des hypotrochoïdes : si deux corps sont en rotation uniforme et de sens contraire dans un plan fixe, la trajectoire apparente de l'un dans un plan lié au deuxième et en translation par rapport au plan fixe est une hypotrochoïde.

Valeur de q	Valeur de
3	2	(voir la surface romaine)
4	3
5	4
5/2	3/2
7/2	5/2
7/3	4/3