Sphère

SPHÈRE
Sphere, Kugelfläche

Du grec sphaira : sphère.

Équation cartésienne : . Équation sphérique : r = R. Paramétrisations cartésiennes :
1) avec ,longitude, latitude.
2) Coordonnées de Mercator, changer sin v en th v dans 1) : ; les courbes v = k u sont les loxodromies de la sphère.
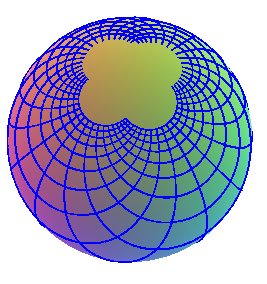
3) Coordonnées stéréographiques de pôle sud : . Les lignes de coordonnées sont les sections de la sphère par les plans passant par les droites x = 0, z = -R et y= 0, z = -R. L'intéret de cette paramétrisation est d'être conforme (conservation des angles).
4) les lignes de coordonnées sont les clélies : , de paramètre .
5)les lignes de coordonnées sont des courbes de Viviani (sections par les cylindres de génératrice Oz de rayons R/2) ; cas p = q = 1 du 4).
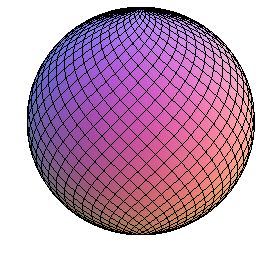5) qui présente la particularité d'être un "habillage" (E = G = 1) de l'hémisphère nord moins l'équateur et le pôle ; une "isométrie" est par contre impossible ( E = G = 1 et F = 0). Les lignes de coordonnées sont étudiées ici.
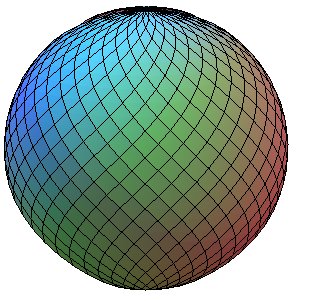
La paramétrisation sphérique : où est une constante et am la fonction amplitude de Jacobi (JacobiAM en Maple), fournit elle aussi un habillage, cette fois de la sphère complète moins les pôles. La pièce de tissu habillant cette sphère est, avant déformation, un carré d'aire , minimale pour .
Première forme quadratique fondamentale : Élément d’aire : . Deuxième forme quadratique fondamentale : Rayons de courbure principaux : R et R. Aire : ; volume : .

La sphère de centre O et de rayon R est le lieu des points de l'espace situés à une distance R de O.
C’est donc la surface engendrée par la révolution d'un cercle autour de son diamètre, qui est un cas limite de tore.
CNS : surface dont tous les points sont des ombilics.

La sphère est une surface homéomorphe au compactifié d'Alexandrov du plan , noté . Autrement dit la sphère moins un point est topologiquement équivalente au plan.

Voir ici le problème de la treizième spère.

Voir aussi l'ellipsoïde, image de la sphère par une transformation affine, et la pseudo-sphère.

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres