PSEUDO-SPHÈRE
Pseudosphere,
Pseudokugel
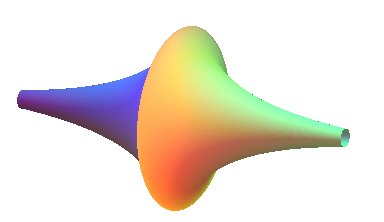
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
PSEUDO-SPHÈRE
Pseudosphere,
Pseudokugel
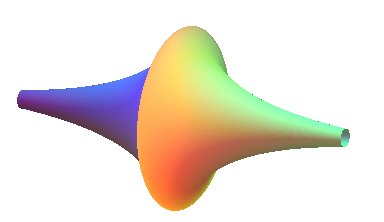

| Surface étudiée par Ferdinand Minding (1806-1885)
et Eugène Beltrami en 1868, ce dernier lui ayant donné le
nom de pseudo-sphère.
Autres noms : surface de Beltrami, tractroïde, tractricoïde. Site : abracadabri. |
| Équation cylindrique : Paramétrisation cartésienne : ou où Paramétrisation où les lignes de coordonnées sont les lignes asymptotiques : Avec la première paramétrisation : Première forme quadratique fondamentale : Courbure méridienne : Courbure de Gauss constante : Volume : |
|
|
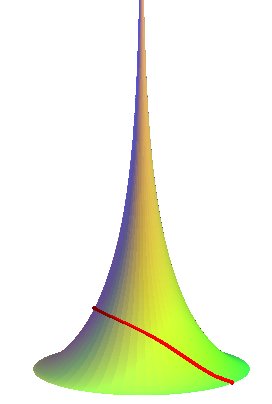
Détermination des géodésiques (Gomes Teixeira tome III p. 271) : l'équation Équation cylindrique des géodésiques : Distance sur la géodésique précédente entre les points de rayons |
 |
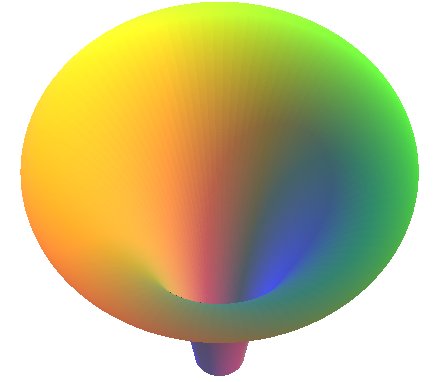
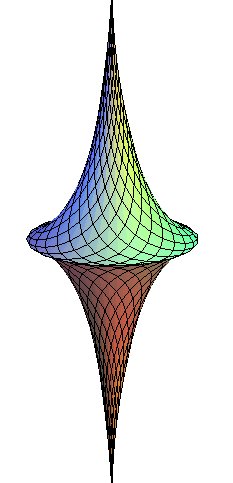
La pseudo-sphère est la surface
de révolution engendrée par la rotation d'une tractrice
autour de son asymptote.
Elle s'appelle ainsi car sa courbure
de Gauss est constante, comme pour la sphère, mais négative
(elle n'est pas la seule surface de révolution de courbure de Gauss
constante négative, voir les autres ici).
Beltrami a considéré cette surface car elle
constitue un modèle du plan hyperbolique.
En effet par un point donné, il passe une infinité
de géodésiques "parallèles", c'est-à-dire,
ne rencontrant pas, une géodésique donnée.
 |
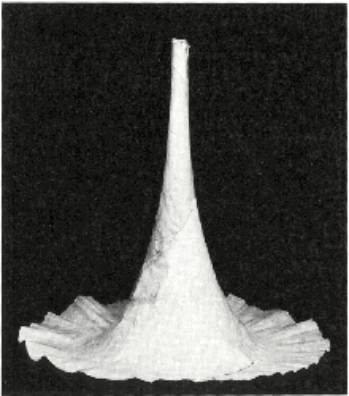
Modèle original de la pseudo-sphère construit par Beltrami. |
Voir aussi l'hélicoïde
pseudosphérique, qui en est une généralisation.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019