SURFACE DE RÉVOLUTION
Surface
of revolution (or rotation surface), Drehfläche (oder Rotationsfläche)
Une surface de révolution est une surface
globalement invariante par toute rotation autour d’une droite fixe appelée
axe
de révolution.
La rotation d’une courbe (appelée génératrice)
autour d’une droite fixe engendre une surface de révolution.
Les sections d’une surface de révolution par des
demi-plans bordés par l’axe de révolution, appelées
méridiennes,
en sont des génératrices particulières.
Les sections par des plans perpendiculaires à
l’axe sont des cercles appelés parallèles de la surface
(une surface de révolution est donc une surface cerclée).
On peut aussi définir les surfaces de révolution
comme les tubes à section variable
dont l'âme est rectiligne, ou comme les enveloppes de sphères
dont les centres sont alignés.
Une surface est une portion de surface de révolution
ssi la normale en tout point rencontre ou est parallèle à
une droite fixe (qui est l'axe de révolution).
Exemples :
- le plan
- les quadriques de révolution : cylindre
de révolution, cône
de révolution, sphère,
ellipsoïde
de révolution, hyperboloïdes (H1
et H2)
de révolution, paraboloïde
de révolution
- le tore
- le caténoïde,
l’onduloïde,
le nodoïde, cas particulier
des surfaces de Delaunay (courbure
moyenne constante)
- la pseudo-sphère
- les surfaces
de révolution à courbure totale constante
- les surfaces
de révolution aux courbures propotionnelles
- la révolution
de la sinusoïde
- la goutte
d'eau pendante
- la trompette
de Gabriel
- la tour
à pression constante
- la surface du solide
d'attraction maximale
- les surfaces
de révolution du huit
- les surfaces
de révolution de la lemniscate de Bernoulli
- la poire de
Tannery
- l'oeuf
double 3D.
Voici un classement suivant la nature de la génératrice
:
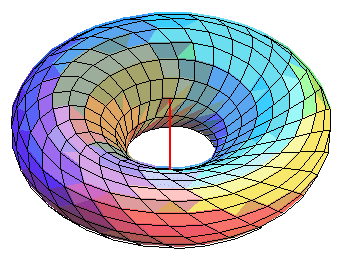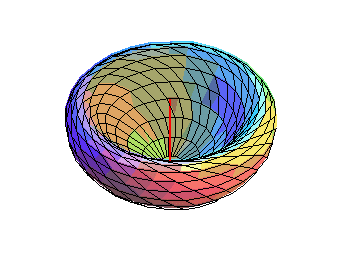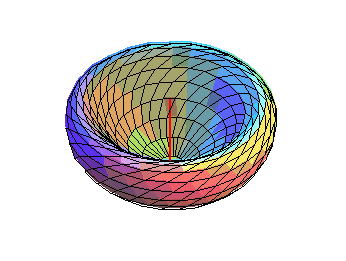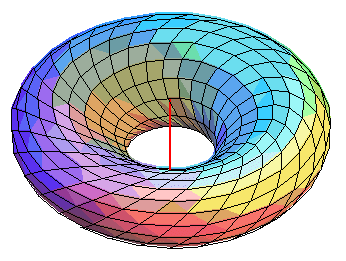 |
Animation montrant la déformation de la surface
de révolution engendrée par la rotation d'un cercle autour
d'un axe, partant d'un tore (engendré par ses cercles de Villarceau),
passant par une demi-sphère, et arrivant sur un tore. |
|
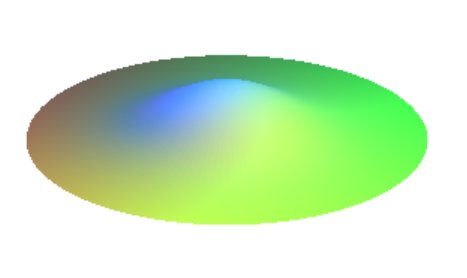
Cubique de révolution d'équation 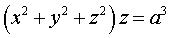 ; sa méridienne est étudiée sur la page de la courbe
d'Agnesi.
; sa méridienne est étudiée sur la page de la courbe
d'Agnesi. |
© Robert FERRÉOL
Alain ESCULIER 2022
où S est l'aire du domaine et d la distance du centre
de gravité du domaine à l'axe.

