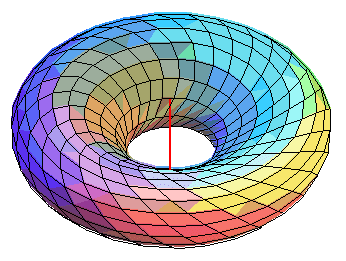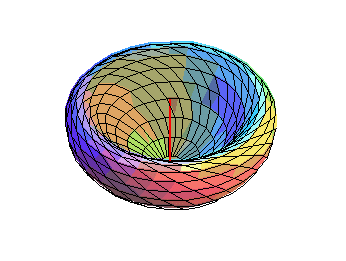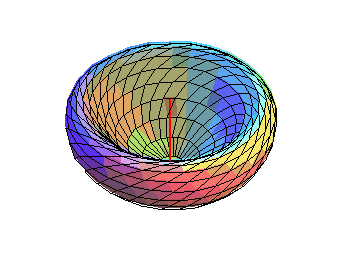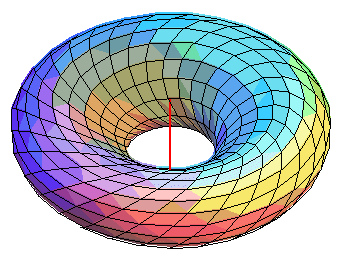
General equation of the surfaces of revolution with axis directed by (a, b, c) :
.
General equation of the surfaces of revolution with axis Oz:
.
Cylindrical equation:
.
Spherical equation:
.
Partial differential equation:
.
Cartesian parametrization:
(generatrix 
).
In particular, for a plane generatrix
: 
(
).
In the latter case:
First fundamental quadratic form:
.
Surface element:
.
Second fundamental quadratic form:
.
Meridian curvature:
; parallel curvature: 
,
where N is the normal to the curve
with respect to the axis Oz.
Gaussian curvature:
;
mean curvature: 
.
The curvature lines are the meridians and the parallels (
).
The cylindrical equation of the asymptotic lines is:
.
The cylindrical equation of the geodesics is:
(see more at geodesics).
Guldin theorems:
The area of the surface of revolution generated by the rotation of an arc of a plane curve around an axis of its plane that does not cross the arc of the curve is equal to
where
l is the length of the arc of the curve and d the distance
from the center of gravity of the arc to the axis.
The volume of the solid of revolution generated
by the rotation of a planar domain around an axis of its plane that does
not cross the domain is equal to 
where S is the area of the domain and d the distance from
the center of gravity of the domain to the axis.
; its meridian curve is studied on the page of the