Revolution of the sinusoid

REVOLUTION OF THE SINUSOID

Surface studied in 2012 by G. Claeser and P. Calvache.
Homemade name, I'm am open to suggestions if you have a better name...

Cylindrical and Cartesian equations: and . Cartesian parametrizations:
1) as a surface of revolution of the sinusoid around Oz: .
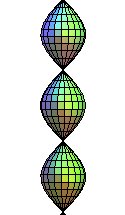2) as a translation surface: , locus of the middles of the segments lines joining the two symmetric circular helices: .
3) as the surface of revolution of one of the previous helices: .

The revolution of the sinusoid is the surface of revolution obtained by rotation of a sinusoid around its axis of translation.

But it is remarkable that surface is also obtained by translation of a circular helix on a symmetric helix with respect to the axis (compare to the right helicoid which is obtained by translation of a helix on itself).
Therefore, it is also obtained by rotation of a circular helix around a generatrix of the cylinder on which it is traced.

The section of this surface by a cylinder tangent to the axis and passing by the vertices is therefore composed of two symmetric circular helices.
Remark (Lapalissade): these helices are the... helices of this surface of revolution....

Obviously, there exist other curves obtained by revolution of a sinusoid, for example: .

Do not mistake for the onduloid, and compare to the egg box.

See on this page a polyhedron with diamond faces that approximates this surface.

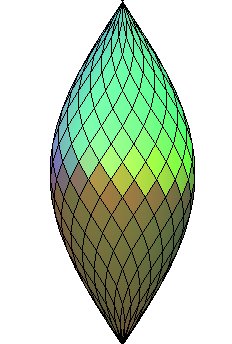
The Gherkin in London, was more or less built on this model.

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra