TRANSLATION SURFACE
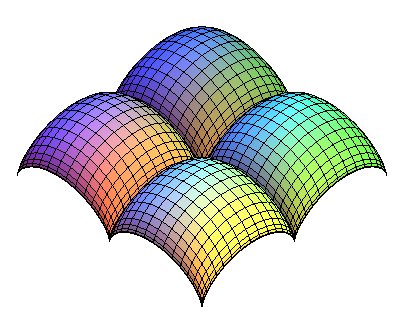
Translation of a cycloid along a cycloid
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TRANSLATION SURFACE

Translation of a cycloid along a cycloid
| Cartesian parametrization: When the generatrices are planes: Cartesian equation (special case): Partial differential equation: |
A translation surface is a surface that is the
union of curves translated images of one another;
It is therefore the resulting surface of the translation
of a curve (first generatrix) along another one (second generatrix); this
definition is symmetric in the sense that the translation of the second
generatrix along the first one results in the same surface.
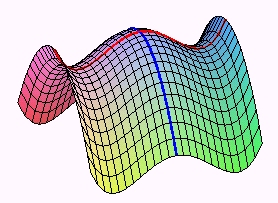 |
For example, the surface |
A translation surface is therefore a special case of Darboux
surface.
If we define the Minkowski sum of two subsets
and
of
the space as the set of points M such that
where
describes
and
describes
,
then a translation surface can be defined as the Minkowski sum of two curves.
We get an equivalent definition by considering the surfaces geometric loci of the middles of the segment lines the ends of which describe two curves ("midsurface").
Examples:
- the plane (case where the two generatrices
are lines)
- the cylinders
(case where the first generatrix is a line)
- the hyperbolic
and elliptic paraboloids
(the two generatrices are parabolas), only translation quadrics.
- the right
helicoid (the two generatrices are circular helices)
- the Bohemian
dome (the two generatrices are circles)
- the egg
box (the two generatrices are sinusoids)
- the revolution
of the sinusoid (the two generatrices are circular helices)
- the Scherk
surface
and the surfaces z = f(x) g(y)?
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017