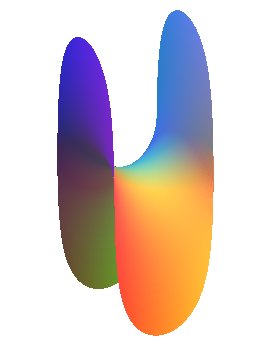
next surface previous surface 2D curves 3D curves surfaces fractals polyhedra

SCHERK SURFACES


Surfaces studied by Scherk in 1834.
Heinrich Ferdinand Scherk (1798-1885): German mathematician.
The minimal helicoids are also sometimes called Scherk surfaces.

First Scherk surface

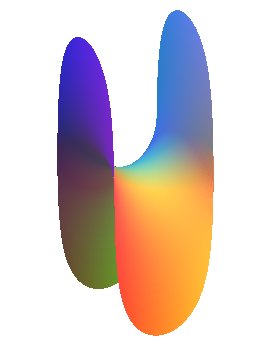
Cartesian equation: , i.e.  , .
Equivalent form: .
Included lines: , and .
Weierstrass parametrization:  with  and , which gives: 
Doubly periodic minimal surface of translation.

The first Scherk surface is the only minimal surface that is a translation surface. It is obtained by translation of the curve of the log cosine (which is also the catenary of equal strength) along itself.

Model of the Scherk surface made by Jean-Marie Dendoncker and his student Julie, model that shows the definition as a translation surface.
 
See here a Scherk surface made of Lego!

 
 

View made with Povray by Alain Esculier
Approximate Scherk surface made of a thin layer of soap;
picture by Jean-Marie Dendoncker.

Compare to the Enneper surface, another minimal surface.

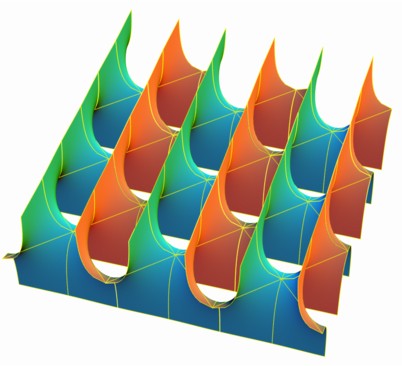
Second Scherk surface

Cartesian equation: . 
Simply periodic minimal surface.

Engraving of the first Scherk surface, by Patrice Jeener, with his kind authorization.


next surface previous surface 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL  2017