RIGHT HELICOID

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
RIGHT HELICOID

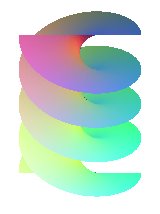
| Surface studied by Meusnier in 1770.
Other names: Meusnier helicoid, surface of the screw with square thread. |
| Cylindrical equation: Cartesian parametrizations:
|
| Cartesian equation: First fundamental quadratic form: Second fundamental quadratic form: Surface element: Gaussian curvature: Equation of the curvature lines: Equation of the geodesics : Area of a coil for a width a: 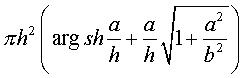 . . |
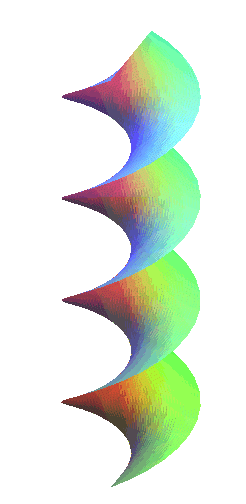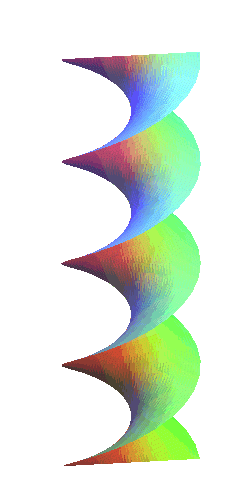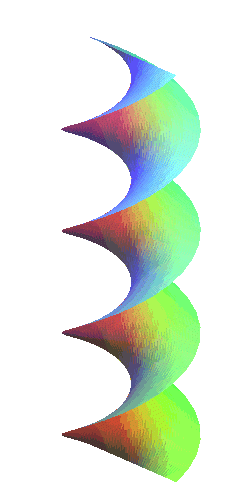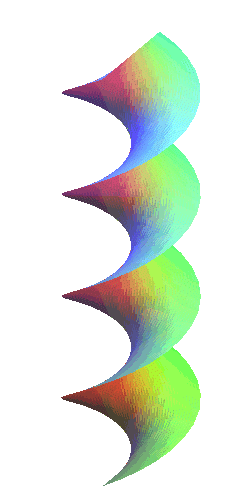 |
The right helicoids are the closed normal ruled
helicoids, in other words, those for which the generatrix is a line
perpendicular (and therefore secant) to the axis. Therefore, they also
are right conoids.
The right helicoid can be obtained as the union of the
principal normals to the circular
helix: .
| The intersection with a cylinder with axis Oz is composed of two circular helices images of one another by a half-turn around the axis Oz, right-handed if h is positive, left-handed otherwise (it is the double helix of the DNA molecule). | 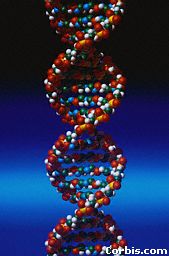 |
| The second parametrization proves that the intersection
between the right helicoid and a full cylinder with axis Oz and
radius a is a translation
surface (a helix sliding on itself); if Oz is vertical, then
these helices are the slope
lines of the helicoid.
Compare to the revolution of a sinusoid. |
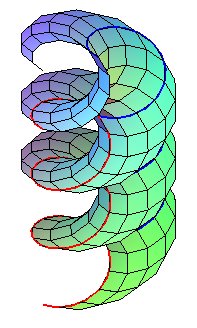 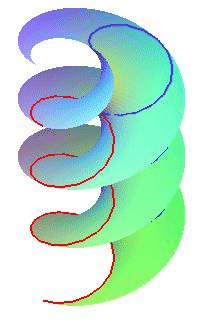 |
| But there are other helices in a right helicoid, with vertical shift equal to half that of the generatrices: the sections by the cylinders passing by the axis! |  |
The right helicoid is, along with the plane, the only
minimal
surface to be ruled (Catalan theorem).
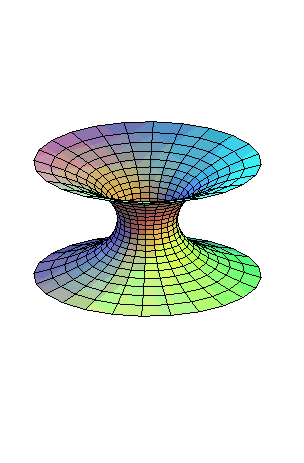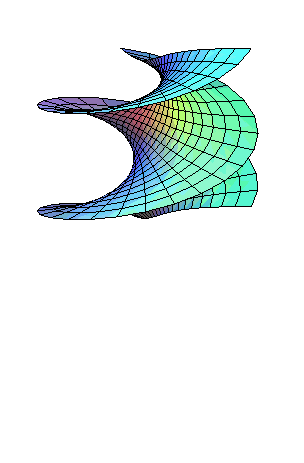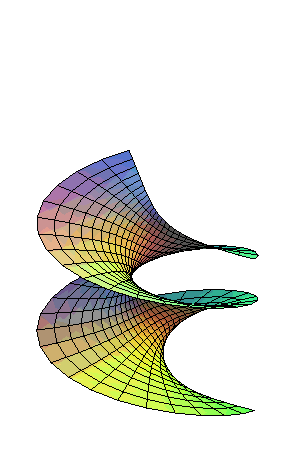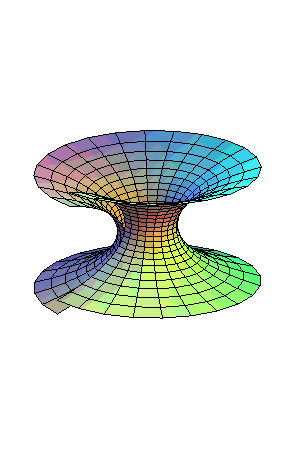
| A right helicoid can be continuously and isometrically
deformed into a catenoid, the
surface remaining constantly minimal and of helical type.
Equations of this transform: The intermediate surfaces are the minimal helicoids. |
 |
| In 1816 Gergonne asked how to split a cube into two parts
by a surface with minimal area fixed to two perpendicular diagonals located
on two opposite faces of the cube.
The answer is not, though one might have thought so, a portion of hyperbolic paraboloid (which would have a linear trace on the faces of the cube), neither the portion of right helicoid (which has a sinusoidal trace on the faces) that joins the two diagonals (Maple: plot3d([u*cos(Pi/4+v)*sqrt(2),u*sin(Pi/4+v)*sqrt(2),(2*v-Pi/2)*2/Pi], u=-1/(sin(Pi/4+v)*sqrt(2))..1/(sin(Pi/4+v)*sqrt(2)), v=0..Pi/2,lightmodel=light2,grid=[20,20]) though it is a minimal surface (but which does not connect at a right angle with the faces of the cube). The answer, given by Schwarz in 1872, is a non-ruled minimal surface the equations of which imply elliptic functions (on the right, the figure drawn by Schwarz himself). See [NITSCHE] p. 77. |
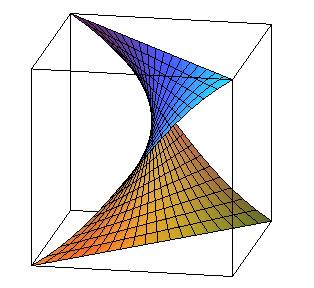 |
| Any plane curve is the projection of the intersection
between a right helicoid and a surface of revolution;
more precisely, the curve with polar equation in xOy : Opposite, for example, the cardioid |
 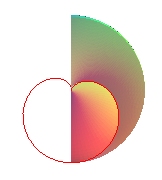 |
See also the Dinostratus
quadratrix.
|
|

Screw with square thread |
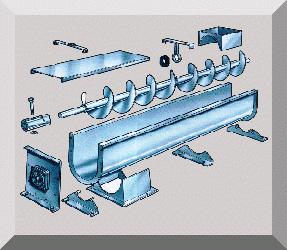
Endless screw |
 
The twisted pasta called "torti" or "fusilli" in Italian are superb helicoids. The example on the right (Barilla) is composed of 3 half-helicoids |
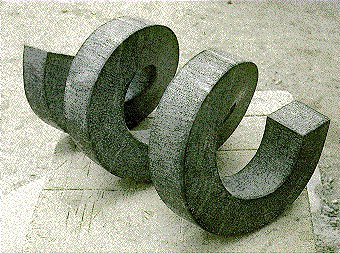
Sculpture by Paul Bloch |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017