Cartesian parametrization:  (where a is the radius of base circle of the helix and its vertical shift is 2pb). . Curvature lines: the generatrices and the level curves.

The developable helicoid is the surface generated by the tangents to a circular helix.
 

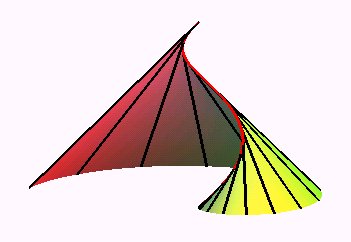
Figure showing the helix and its half-tangents.

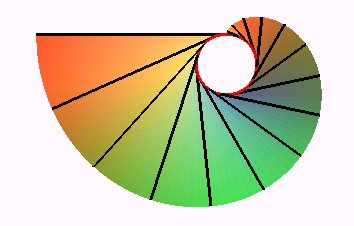
View from below

It is a surface of equal slope (like any surface generated by the tangents to a helix), and it is the only helicoid to be developable.
Being generated by a line of a rolling plane without sliding on a cylinder of revolution, it is a molding surface.
 

The level curves (sections by horizontal planes) are involute of circles; they are the involutes of the cuspidal edge (which is a helix) as well as the involutes of the cylinder that contains the helix.

 

The parametrization of the section by the plane y = 0 is: ; the developable helicoid is therefore the result of the helical movement of this curve along its axis:

 

Modeling of the developable helicoid by Robert March, professor at the Paris school of architecture, who also proposes the following concrete production: take a tinfoil roll, unwind a length of foil equal to its width, form a right triangle by folding diagonally, re-wind, and unwind again while keeping the foil tight; the diagonal generates the developable helicoid and its tip a beautiful involute of a circle.

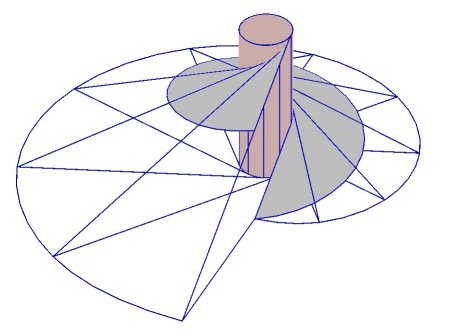Entrance staircase of the Louvre by the Pyramid. Of course, the stairs generate a right helicoid but the surface under the staircase (the intrados) is a portion of a developable helicoid. Notice indeed that the visible outline of the surface is composed of linear generatrices (cf. red lines).

 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017