Cartesian parametrization, for a generatrix at distance a from the axis Oz and forming an angle  with the horizontal:  ("inside helix": ). closed helicoid: a = 0; normal helicoid: ; developable helicoid: .

The ruled helicoids are the helicoids a generatrix of which is a straight line, in other words, the surfaces generated by the helical motion of a line (D) around an axis Oz.

When the translation of the helical motion is zero (h = 0), we get as a limit case the hyperboloid of revolution, or even the cone of revolution, the cylinder of revolution or the plane.

The helicoid is said to be closed when (D) is secant to the axis, open otherwise (the complement of the helicoid then contains a cylinder of revolution with same axis).

When (D) is orthogonal to the axis, the directrix cone of the ruled helicoid (which always is of revolution) becomes a plane hence the name helicoid with directrix plane or normal helicoid; a helicoid that is at the same time normal and closed is called a right helicoid.

When the line is neither orthogonal nor parallel to the axis, we get the helicoid with directrix cone. In this case, the point P, foot on (D) of the common perpendicular of (D) and the axis, describes a circular helix, called "inside helix", which is the striction line; when the line (D) remains tangent to this helix, we get the developable helicoid. A closed helicoid with directrix cone is also called "surface of the screw with triangular thread".
 
 

		normal helicoid
closed helicoid
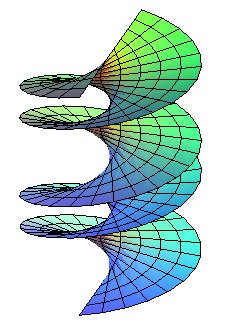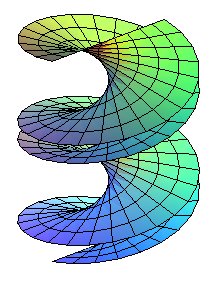open helicoid

 

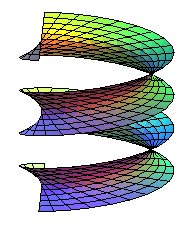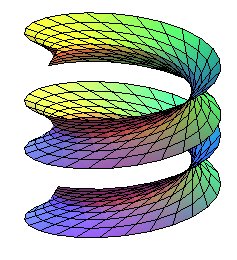The faces of the helical "prisms" opposite are portions of open normal ruled helicoids. The view on the right is a work by Anish Kapoor from 2014. See at rotoid the circular version of these solids.

 

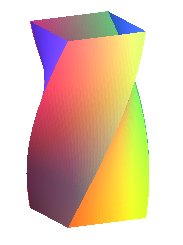next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017