PRISME
Prism, Prisma
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
PRISME
Prism, Prisma

| Du grec prisma "prisme", provenant du verbe prizein
"scier".
Lien : mathematische-basteleien.de/prisma.htm |
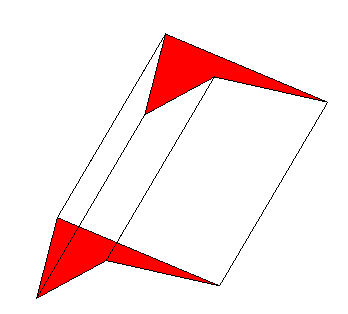
Un prisme est un polyèdre ayant deux faces parallèles (ses bases) dont les sommets sont joints 2 à 2 par des arêtes, formant les faces latérales, qui doivent être des parallélogrammes. Le prisme est dit droit lorsque les faces latérales sont rectangulaires. L'ordre du prisme est celui de ses bases.
Les prismes sont aux polyèdres ce que les cylindres
sont aux surfaces (tandis que les pyramides
sont aux polyèdres ce que les cônes
sont aux surfaces) : la réunion des faces latérales d'un
prisme forme un tronc de cylindre.
| Le dual d'un prisme convexe est une bipyramide (ou diamant) du même ordre. | 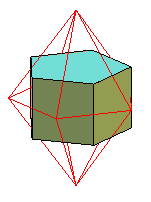 |
Un parallélépipède
est de 3 façons différentes un prisme.
| Le seul prisme qui soit un polyèdre régulier est le cube, et il y a, pour un ordre donné, un seul prisme à faces régulières, qui est un polyèdre semi-régulier. Cependant, on désigne couramment par "prisme régulier" un prisme droit de base un polygone régulier ; les faces latérales sont alors des rectangles. |   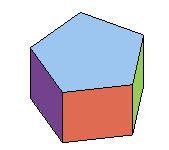 |
| Pour un prisme régulier convexe de rayon R
et de hauteur h, l'aire de la base est Pour n = 3, |

Prisme triangulaire à faces de même aire. |
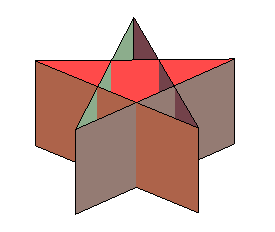
On peut étendre la notion de prisme au cas de bases qui sont des polygones croisés.
Voir aussi les antiprismes,
les hyperprismes, les équidomoïdes,
les prismes
hélicoïdaux.
 |

Les plus célèbres prismes triangulaires et hexagonaux... |
 |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2025