Paramétrisation cartésienne, pour une génératrice à distance a de l'axe Oz et faisant un angle  avec l'horizontale:  Paramétrisation de l'hélice de gorge : . Hélicoïde fermé : a = 0 ; hélicoïde normal :  ; hélicoïde développable : .

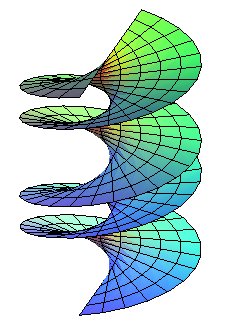
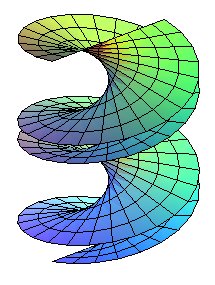
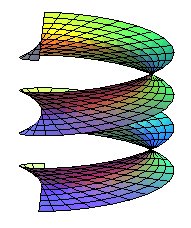
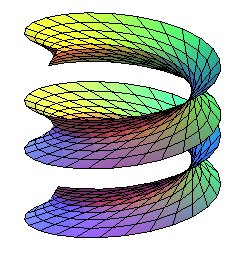
Les hélicoïdes réglés sont les hélicoïdes dont une génératrice est une droite, autrement dit, les surfaces engendrées par le mouvement hélicoïdal d’une droite (D) autour d’un axe Oz.

Lorsque le mouvement hélicoïdal a une translation nulle (h = 0), on obtient comme cas limite l’hyperboloïde de révolution, voire le cône de révolution, le cylindre de révolution ou le plan.

L'hélicoïde est dit fermé quand (D) est sécante à l'axe, ouvert sinon (le complémentaire de l'hélicoïde contient alors un cylindre de révolution de même axe).

Lorsque (D) est orthogonale à l’axe, le cône directeur de l'hélicoïde réglé (qui est toujours de révolution) devient un plan d'où le nom d’hélicoïde à plan directeur ou hélicoïde normal ; un hélicoïde à la fois normal et fermé est appelé hélicoïde droit.

Lorsque la droite n’est ni orthogonale ni parallèle à l’axe, on obtient l’hélicoïde à cône directeur. Dans ce cas, le point P, pied sur (D) de la perpendiculaire commune à (D) et à l’axe, décrit une hélice circulaire dite "hélice de gorge", qui est la ligne de striction ; lorsque la droite (D) reste tangente à cette hélice, on obtient l’hélicoïde développable. (et parfois appelé pseudo-développable dans le cas général). Un hélicoïde à cône directeur fermé est aussi désigné par "surface de la vis à filet triangulaire".
 
 

		hélicoïde normal
hélicoïde fermé
hélicoïde ouvert

 

Les "prismes" hélicoïdaux ci-contre ont pour faces des portions d'hélicoïdes réglés normaux ouverts. La vue de droite est une oeuvre d'Anish Kapoor de 2014. Voir à rotoïde la version circulaire de ces solides.

 

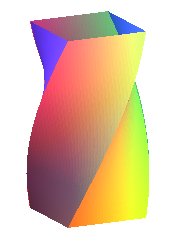surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2018