HÉLICOÏDE DROIT
Right
helicoid, Wendelfläche

| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
HÉLICOÏDE DROIT
Right
helicoid, Wendelfläche

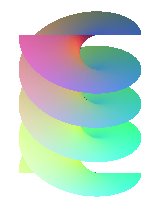
| Surface étudiée par Meusnier en 1770.
Autres noms : hélicoïde de Meusnier, surface de la vis à filet carré, hélicoïde à plan directeur fermé. |
| Équation cylindrique : Équation cartésienne : Paramétrisations cartésiennes :
|
| Première forme
quadratique fondamentale : Deuxième forme quadratique fondamentale : Élément d'aire : Courbure de Gauss : Équation des lignes de courbure : Équation des géodésiques : Aire d'une spire sur une largeur a : 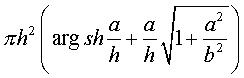 . . |
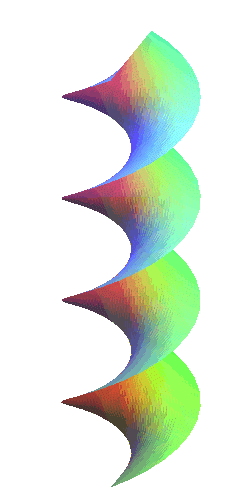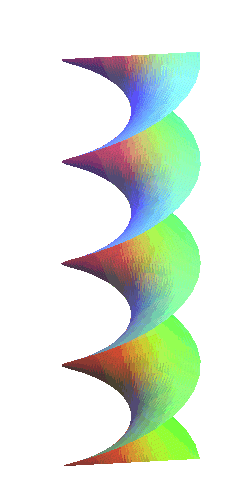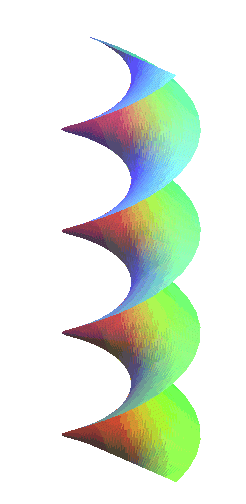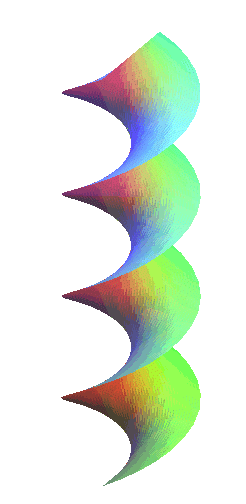 |
Les hélicoïdes droits sont les hélicoïdes
réglés normaux fermés, autrement dits ceux dont
la génératrice est une droite perpendiculaire (donc sécante)
à l’axe. Ce sont donc aussi des conoïdes
droits.
L'hélicoïde droit s'obtient comme réunion
des normales principales à l'hélice
circulaire : .
| L’intersection avec un cylindre d'axe Oz est formé de deux hélices circulaires images l’une de l’autre dans un retournement d’axe Oz, dextres si h est positif, senestres sinon (c’est la double hélice de la molécule d’ADN). | 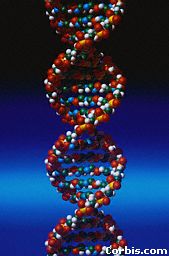 |
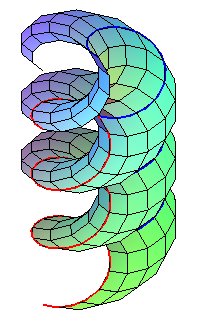
| La deuxième paramétrisation montre que
l’intersection de l'hélicoïde droit avec un cylindre plein
d’axe Oz et de rayon a est une surface
de translation (une hélice glissant sur elle-même) ; si
Oz
est vertical, ces hélices sont les lignes
de pente de l'hélicoïde.
Comparer avec la révolution de la sinusoïde. |
 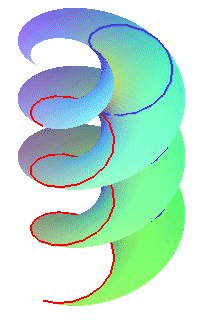 |
| Mais il y a d'autre hélices dans un hélicoïde droit, de pas moitié de celui des hélices génératrices : les sections par des cylindres passant par l'axe ! |  |
L’hélicoïde droit est, avec le plan la seule
surface
minimale qui soit réglée (théorème de Catalan).
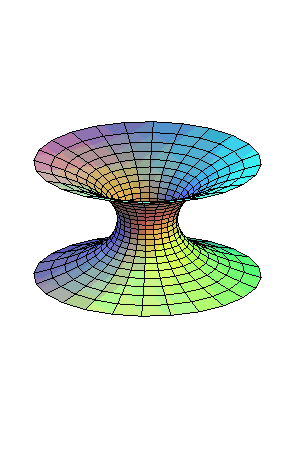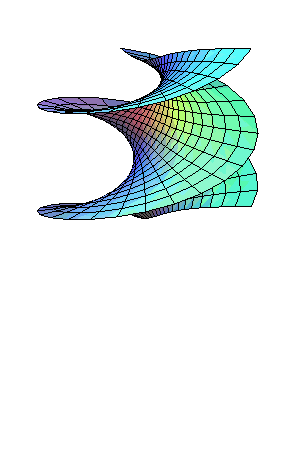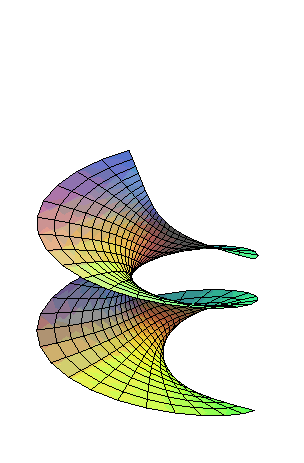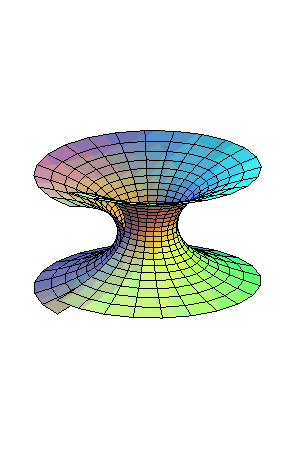
| Un hélicoïde droit peut être transformé
continûment et isométriquement en un caténoïde,
la surface restant constamment minimale et de type hélicoïdal.
Équations de cette transformation : Les surfaces intermédiaires sont les hélicoïdes minimaux. |
 |
| En 1816 Gergonne demandait comment partager un cube en
deux parties par une surface d'aire minimale fixée à deux
diagonales orthogonales situées sur deux faces opposées du
cube.
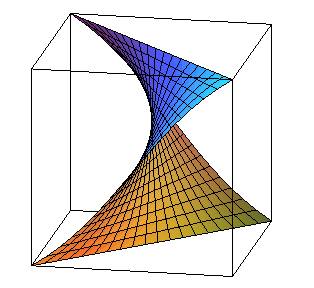
La réponse n'est pas, comme on pourrait le penser, une portion de paraboloïde hyperbolique (qui aurait une trace rectiligne sur les faces du cube), ni même la portion d'hélicoïde droit (qui a une trace sinusoïdale sur les faces), qui joint les deux diagonales (maple : plot3d([u*cos(Pi/4+v)*sqrt(2),u*sin(Pi/4+v)*sqrt(2),(2*v-Pi/2)*2/Pi], u=-1/(sin(Pi/4+v)*sqrt(2))..1/(sin(Pi/4+v)*sqrt(2)), v=0..Pi/2,lightmodel=light2,grid=[20,20]) qui est pourtant une surface minimale (mais ne se raccorde pas à angle droit sur les faces du cube). La réponse, donnée par Schwarz en 1872, est une surface minimale non réglée dont les équations font intervenir des fonctions elliptiques (à droite, figure dessinée par Schwarz lui-même). Voir [NITSCHE] p. 77. |
 |
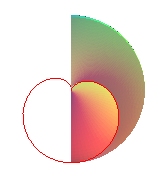
| Toute courbe plane est la projection de l'intersection
d'un hélicoïde droit avec une surface de révolution
;
plus précisément, la courbe d'équation polaire dans xOy : Ci-contre par exemple, la cardioïde |
  |
Voir aussi à quadratrice
de Dinostrate.
|
|

Vis à filet carré |
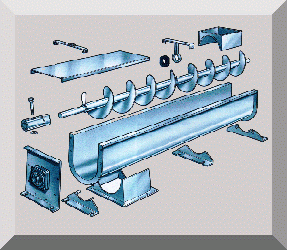
Vis sans fin |
 
Les pâtes torsadées appelées "torsettes", "torti" ou "fusilli" en italien sont de superbes hélicoïdes. L'exemple de droite (Barilla) est formé de 3 demi-hélicoïdes |
Sculpture de Paul Bloch |
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019