Équation cartésienne générale d'un conoïde d'axe intersection des plans d'équation Q = 0 et R = 0, de plan directeur d'équation P = 0 :  avec f homogène par rapport à ses deux premières variables. Équation cartésienne générale d'un conoïde d'axe Oz et de plan directeur z = mx : f(x, y, z – mx) = 0  avec f homogène par rapport à (x, y), le conoïde étant droit pour m = 0. En résolvant en z on obtientavec g homogène par rapport à (x, y), ce qui donne pour Équation cylindrique : . Paramétrisation cartésienne :  (). Ligne de striction :  avec  (ligne égale à l'axe pour un conoïde droit). Première forme quadratique fondamentale dans le cas droit : . Équation cartésienne du conoïde d'axe Oz, de plan directeur z = mx et de directrice la courbe (C) d'équation f(y, z) = 0 dans le plan x = a :  Si (C) est algébrique de degré n, le conoïde est algébrique de degré compris entre n et 2n. Paramétrisation cartésienne du conoïde d'axe Oz, de plan directeur z = mx et de directrice la courbe :  dans le plan x = a : . Paramétrisation cartésienne simple du conoïde droit d'axe Oy et de directrice la courbe :  dans le plan x = a : .

Exemples de conoïdes algébriques :
degré 2 : le paraboloïde hyperbolique, qui est doublement un conoïde
degré 3 : toutes les surfaces cubiques réglées, dont le conoïde de Plücker, celui de Zindler et les conoïdes paraboliques.
degré 4 : le coin conique.

Exemples de conoïdes transcendants :
    - l'hélicoïde droit.
    - le conoïde sinusoïdal, ou surface de Gaudi.

Quelques exemples visuels :
 

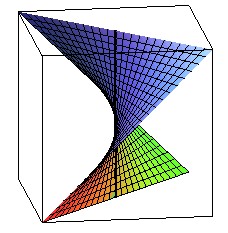
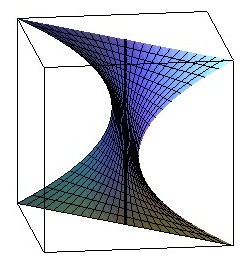
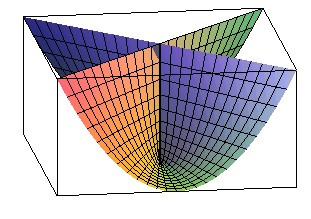
Conoïde droit de directrice une droite ni parallèle, ni perpendiculaire à l'axe : paraboloïde hyperbolique équation : z =  y /x.	Conoïde droit de directrice une parabole d'axe perpendiculaire à celui du conoïde : voir à conoïde parabolique. équation : z² = y/x	Conoïde droit de directrice une parabole d'axe parallèle à celui du conoïde : parapluie de Whithney équation : z = (y/x)²

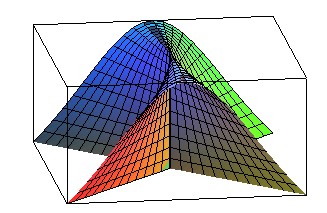
Conoïde droit de directrice une cubique d'Agnesi : conoïde de Plücker. equation : z = (1 - (y/x)²)/(1 + (y/x)²).	Conoïde droit de directrice un cercle dans un plan parallèle à l'axe : coin conique. équation : z² + (y/x)^2 = 1

 

On peut généraliser la notion de directrice à une surface : le conoïde est alors défini comme réunion des droites passant par l'axe, parallèles au plan directeur, et tangentes à la surface directrice. Par exemple, voici le cas où la surface directrice est la sphère de rayon b centrée en (a, 0, 0), le plan directeur xOy, et l'axe Oz : Équation cartésienne : (comparer avec le coin conique : ). Équation cylindrique : . Paramétrisation cartésienne :. Paramétrisation de la courbe de tangence avec la sphère :. Lorsque b = a on obtient le conoïde de Plücker d'ordre 1.

 

Toute courbe plane est la projection de l'intersection d'un certain conoïde avec un cône de révolution ; plus précisément, la courbe d'équation polaire dans xOy  est la projection sur xOy de l'intersection du conoïde  avec le cône de révolution . Ci-contre par exemple, la cardioïde est la projection de l'intersection du conoïde de Plücker :  avec le cône de révolution .

On désigne parfois par surface conoïdale une surface réglée ayant deux directrices rectilignes : le conoïde est alors le cas où l'une de ces directrices est à l'infini.
L'image par une homographie d'une surface conoïdale (donc en particulier d'un conoïde) est une surface conoïdale.
Le berlingot est un exemple de telle surface.
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2020