Nom maison. Surface étudiée par Cundy et Rollett en 1951 [Cundy Rollett p 185 à 188] Voir aussi un modèle en fils du National Museum of American History.

 

Paramétrisation cartésienne : . Équation cartésienne :  (montrant que les courbes de niveau sont des ellipses), soit . Surface quartique, avec deux droites doubles : . Volume du berlingot : . Aire du berlingot pour k = 1/2  : » 7,29a2. La ligne de striction est obtenue pour , d'où la paramétrisation : .

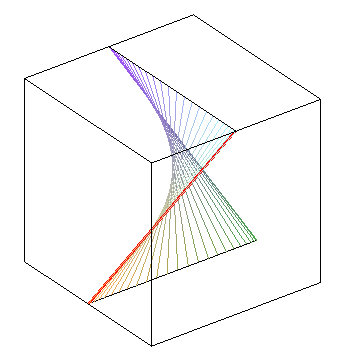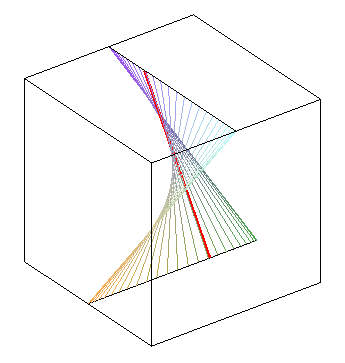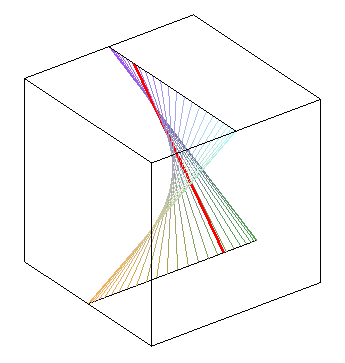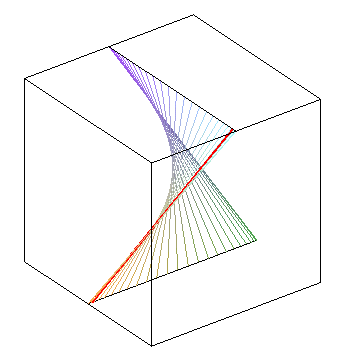
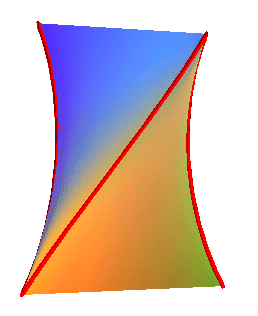Berlingot avec sa ligne de striction, qui se projette en une astroïde. [Aubert Papelier, T 3, p. 132].

 
 

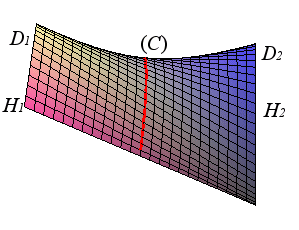
Étant donné deux droites (D1) et (D2) orthogonales non sécantes, (H1H2) leur perpendiculaire commune, O le milieu de [H1H2] et (C) un cercle de centre O de plan parallèle à (D1) et (D2), le berlingot est la surface réglée non développable engendrée par les droites rencontrant (D1), (D2) et (C) ; c'est donc une surface conoïdale. Ici, (D1) est  , (D2) est  et (C) est de rayon ka.
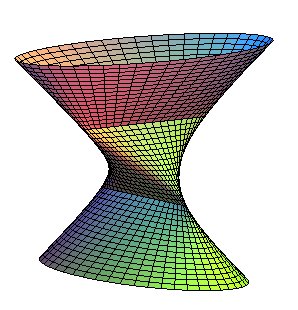
Voici la surface (plus) complète. Les deux segments doubles portés par (D1) et (D2) sont de longueur 4ka.

 

Le berlingot est aussi la surface réglée engendrée par les droites (M1M2),  et  ayant deux mouvements sinusoïdaux orthogonaux en quadrature ; la partie ayant la forme de berlingot est la réunion des segments [M1M2]. La longueur du segment [M1M2] reste alors constante égale à  ; le berlingot peut donc aussi être défini comme la surface réglée engendrée par une droite dont deux points fixes coulissent sur deux droites fixes orthogonales non sécantes. Tous les points de la droite décrivent des ellipses (ce qui constitue une généralisation de l'ellipsographe de Proclus).

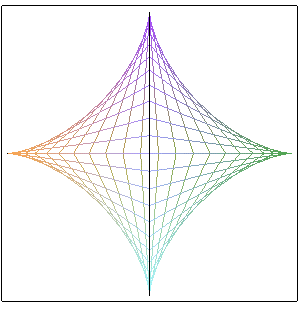
La projection du segment [M1M2] sur xOy garde aussi une longueur constante : la vue de dessus d'un berlingot est donc une astroïde pleine.

On obtient donc aussi une généralisation du berlingot en considérant la surface conoïdale engendrée par les droites (M₁M₂), ,  ayant deux mouvements sinusoïdaux orthogonaux en déphasage quelconque (le berlingot étant obtenu pour ).
 

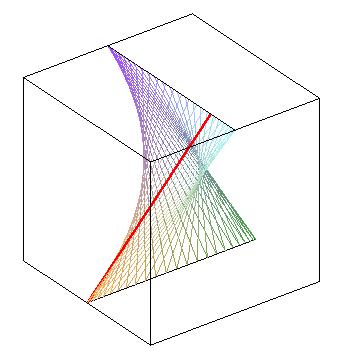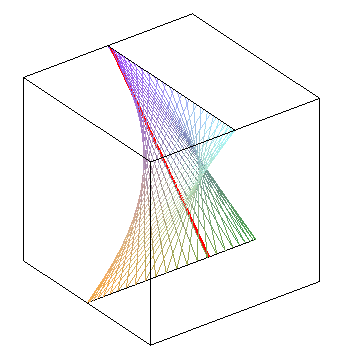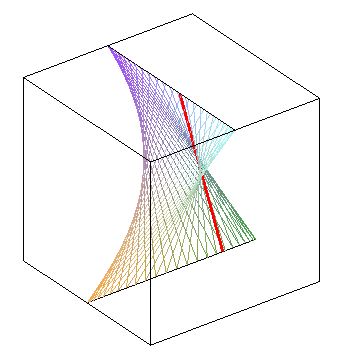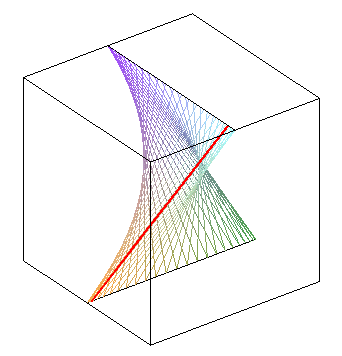
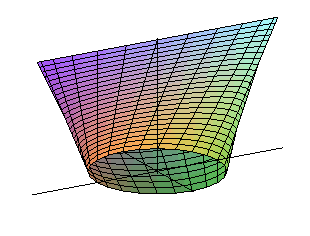
déphasage de	déphasage nul : on obtient un paraboloïde hyperbolique	opposition de phase : autre paraboloïde hyperbolique

 

Attention, un berlingot tetrapack comme ci-contre fabriqué avec du papier est une surface développable, fabriquée avec un patron de tétraèdre, en arrondissant les arêtes... Et ces bonbons berlingots  sont beaucoup plus arrondis !

Comparer avec le coin conique, ainsi que la surface tétraédrique de Cayley.

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Alain ESCULIER 2022