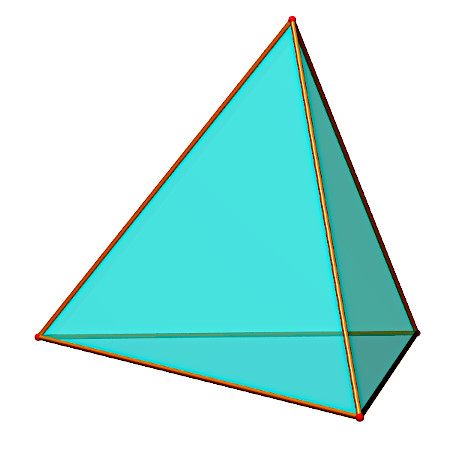
Un tetraèdre est un polyèdre à 4 faces (ou 4 sommets), nombre minimal possible ; il n'en existe qu'un seul type, équivalent au tétraèdre régulier dont voici la carte de visite :
 
 

Famille	polyèdres réguliers également pyramides
Historique	découvert avant ou après le cube ????
Dual	lui-même 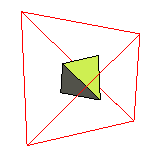¬ dual polaire du tétraèdre par rapport à sa sphère circonscrite
Faces	4 triangles
Sommets	4 sommets de degré 3, de code de Schläfli 33
Arêtes	6 arêtes de longueur a ; angle dièdre : rd, soit 70° 31' 44"
Patrons
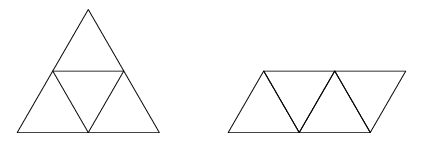Graphe (diagramme de Schlegel)	graphe complet d'ordre 4 K4 :
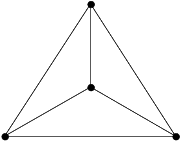Diamètres	sphère inscrite :  ; intersphère (tangente aux  arêtes) : ; sphère circonscrite :  .
Mensurations	volume :  ; aire :  ; rapport volume/(volume de la sphère circonscrite) : 12% coefficient isopérimétrique :
Coordonnées  des sommets	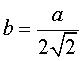() avec un nombre pair de signes - (cas du tétraèdre 1 passant par (b,b,b) - ou un nombre impair pour le tétraèdre 2 passant par (-b,-b,-b)), tous les sommets étant reliés entre eux
Équations cartésiennes des plans faces	avec un nombre impair de signes - pour le tétraèdre 1 (ou un nombre pair pour le tétraèdre 2)
Équation de la surface du tétraèdre 1	(bord de l'intersection de 4 demi-espaces) ou  (bord de l'intersection de 4 bandes)
Équation du tétraèdre 1 plein	(exprimant le fait que la somme des distances d'un point intérieur aux faces du tétraèdre est constante, généralisation du théorème de Viviani).
Construction	troncature maximale d'un sommet du cube sur deux :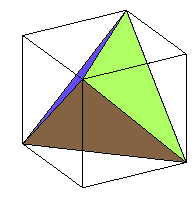
Plans de symétrie	6 plans médiateurs, passant par les 6 arêtes.
Axes de rotation	les 4 hauteurs (2 rotations d'ordre 3 par axe) les 3 médianes, joignant les milieux de 2 arêtes opposées (une rotation d'ordre 2 par axe). Noter que d'après la figure ci-contre, la carré est donc le projeté d'un tétraèdre régulier !
Groupe des isométries	ordre 24 : 12 rotations et 12 antirotations ce groupe est isomorphe à S4 (action simple et transitive sur les 4 sommets, ou les 4 faces). Isométries permutations sur les sommets correspondantes 12 rotations : identité, 8 tiers de tours, 3 demi-tours 12 permutations paires : identité, 8 cycles d'ordre 3, 3 produits de 2 transpositions disjointes 12 antirotations : 6 réflexions, 6 réflexions-rotations d'angle droit 12 permutations impaires : 6 transpositions, 6 cycles d'ordre 4.
Pavage	Le tétraèdre régulier ne pave pas l'espace, mais il le fait en association avec l'octaèdre régulier.
Polyèdres dérivés	par troncature forte : octaèdre ; par troncature faible : tétraèdre tronqué ; par chanfreinage : cuboctaèdre ; par adoucissement : icosaèdre ; par augmentation : triaki-tétraèdre .
Avatars	le tétraèdre de Sierpinski, le tétraèdre de Reulaux, la surface de Kümmer.

 

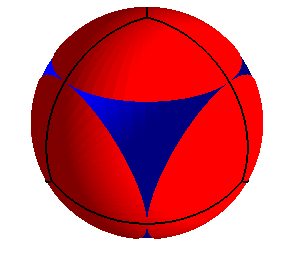Le tétraèdre régulier donne une réponse au problème dit "des dictateurs ennemis" dans le cas n = 4 : quel est la taille maximale de n calottes sphériques identiques (les états de chaque dictateur) de sorte qu'elles puissent se répartir sur une sphère sans se chevaucher, et quelle est alors leur disposition ? Réponse : les 4 calottes maximales ont un angle au centre de rd, soit 109° 28' 16" et sont centrées aux sommets d'un tetraèdre régulier. Les états occupent alors 61 % de la surface totale. Sources : Marcel Berger, pour la Science 176, p. 72 et dossier Pour la Science 41 p. 40. La figure ci-contre montre également que le squelette de l'octaèdre régulier fournit, par projection sur la sphère circonscrite, un pavage régulier de la sphère par 4 triangles équilatéraux sphériques.

 

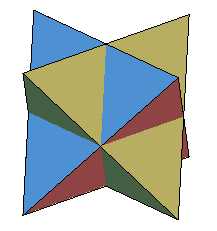
Le tétraèdre et son symétrique par rapport à son centre forment un polyèdre composé appelé stella octangula par Képler, octangle étoilé en francais ; ses sommets sont ceux d'un cube et la partie commune est un octaèdre.
La surface de Cayley : pour  fournit un beau tétraèdre aux arêtes arrondies. Voir plus généralement les surfaces cubiques ayant les symétries du tétraèdre à surface de Goursat.

Voir aussi la généralisation au simplexe.

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2011