Solides découverts par Théétète d'Athènes au quatrième siècle avant J.C. Autres noms : solides de Platon, ou platoniciens. Site :  polyhedra.mathmos.net/entry/platonicsolids.html

Un polyèdre est dit régulier si toutes ses faces sont des polygones réguliers de même type et si tous ses sommets sont de même degré.

Un drapeau étant une suite  où f est une face, a une arête de cette face, et s une extrémité de cette arête, le polyèdre est régulier ssi le groupe des isométries laissant le polyèdre invariant est transitif sur les drapeaux, c'est-à-dire qu'il existe toujours une isométrie envoyant un drapeau donné sur un drapeau donné. Plus concrètement, cela se traduit par le fait que si l'on fabrique une boîte moulant entièrement le polyèdre, si l'on marque dans la boite une face, une arête de cette face et une extrémité de cette arête, et si l'on fait de même sur le polyèdre, le polyèdre pourra toujours y être rangé en appliquant face marquée contre face marquée, arête contre arête, et sommet contre sommet.

Autres CNS :
    - polyèdre semi-régulier dont les faces sont de même ordre
    - polyèdre semi-régulier de deuxième espèce dont les sommets sont de même degré.
 

Attention : un polyèdre dont toutes les faces sont des polygones réguliers de même type n'est pas forcément régulier : par exemple :  la bipyramide  à base triangulaire et faces régulières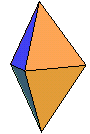(sommets de degré 3 ou 4),
et plus généralement, tous les deltaèdres.

Un polyèdre régulier possède les régularités suivantes :

Concernant les faces :
    1a) toutes les faces ont même ordre
    1b) toutes les faces ont la même aire
    1c) toutes les faces sont isométriques
    1d) toutes les faces sont régulières

Concernant les sommets :
    2a) tous les sommets ont même degré
    2b) les angles solides aux sommets sont tous égaux
    2c) tous les sommets sont isométriques en ce sens que les figures formées par les demi-droites issues de chaque sommet sont isométriques.
    2d) tous les sommets sont réguliers (les angles des faces arrivant en un même sommet sont égaux)

Concernant les arêtes :
    3a) toutes les arêtes ont même longueur
    3b) tous les angles dièdres sont égaux

Bon exercice : quels sous-ensembles de conditions ci-dessus caractérisent les polyèdres réguliers ?

Un polyèdre régulier (avec la définition des polyèdres donnée dans ce site) est convexe, inscriptible et circonscriptible (plus précisément, il possède une sphère tangente à chaque face en son centre).

Il existe à similitude près cinq polyèdres réguliers (théorème de Platon) décrits dans le tableau ci-dessous :

Rem : le code de Schläfli de chaque sommet d'un polyèdre régulier est le même, et de la forme p^q (q p-gones arrivant à chaque sommet),
et on désigne par symbole de Schläfli, qui se généralise aux dimensions supérieures, la notation légèrement différente : {p, q].
 

nom	code et symbole de Schläfli	faces	sommets	arêtes	remarque	figure
tétraèdre régulier	33  {3,3}	4 triangles	4 de degré 3	6	auto-dual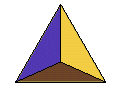
cube	43  {4,3}	6 carrés	8 de degré 3	12	dual de l'octaèdre
octaèdre (régulier)	34  {3,4}	8 triangles	6 de degré 4	12	dual du cube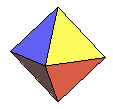
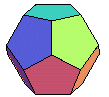
dodécaèdre (régulier)	53  {5,3}	12 pentagones	20 de degré 3	30	dual de l'icosaèdre
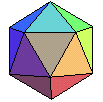
icosaèdre (régulier)	35  {3,5}	20 triangles	12 de degré 5	30	dual du dodécaèdre

Il est remarquable que la donnée du symbole de Schläfli {p , q} et de la longueur d'arête a définit entièrement le polyèdre régulier, à isométrie près.
On peut du reste exprimer par des formules communes les données concernant les 5 polyèdres réguliers, en fonction de la longueur de l'arête a, de l'ordre p des faces et du degré q des sommets (S et F étant déjà reliés par : q S = p F).
 

Nombre de sommets	Nombre d'arêtes	Nombre de faces

 

Diamètre de la sphère inscrite	Diamètre de l'intersphère (tangente aux arêtes)	Diamètre de la sphère circonscrite

 

Angle dièdre entre deux faces adjacentes	Aire totale	Volume

Les 5 polyèdres réguliers correspondent aux 5 pavages possibles de la sphère par des polygones sphériques réguliers (à 3 arêtes au moins), isométriques, bord à bord, et dont tous les sommets sont du même type, que nous relions ci-dessous aux 3 seuls pavages du plan par des polygones réguliers ayant des propriétés similaires.

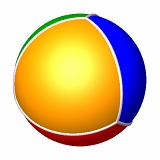
Tout d'abord, 3+1 pavages triangulaires ou deltillages (images réalisées par Alain Esculier) :

deltillage 33 correspondant au tétraèdre	deltillage 34 correspondant à l'octaèdre	deltillage 35 correspondant à l'icosaèdre	deltillage 36 plan

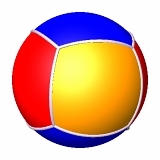
1+1 pavages carrés, ou quadrillages :

quadrillage 43 correspondant au cube	quadrillage 44 plan

1 pavage pentagonal ou pentillage sphérique et 1 pavage hexagonal ou hexillage plan :

pentillage 53 correspondant au dodécaèdre	hexillage 63 plan Voir ici une application au nombre chromatique du tore	Superbe pavage hexagonal à la mosquée Bleue de Tabriz (Iran, Azerbaïdjan Oriental). Photo, Alain Juhel.

REM 1: il existe aussi sur la sphère des polygones à deux arêtes d'aire non nulle : les hosoèdres qui donnent lieu à d'autres pavages.

REM 2 : Il existe encore 4 polyèdres généralisés réguliers, dits "polyèdres réguliers étoilés", ou "polyèdres de Képler-Poinsot".

Pour d'autres généralisations, voir les polyèdres semi-réguliers, les polychores réguliers, les polytopes réguliers.
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2014