Etymologie	Du grec Kubos : dé
Définitions	un cube est        - un polyèdre à faces carrées        - un hexaèdre régulier        - un parallélépipède rectangle à arêtes de même longueur        - un prisme droit à base carrée et faces latérales carrées.        - un antidiamant d'ordre 3 à sommets réguliers et angles dièdres égaux.
Famille	polyèdres réguliers également : paralléloèdres
Dual	octaèdre régulier 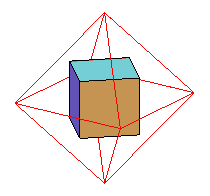¬ dual polaire du cube par rapport à sa sphère circonscrite
Faces	6 carrés
Sommets	8 sommets de degré 3, de code de Schläfli 43; angle solide : sr
Arêtes	12 arêtes de longueur a ; angle dièdre :  rd
Patrons
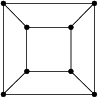Graphe des arêtes	Voir d'autres représentations sur mathworld.
Diamètres	sphère inscrite : a ; intersphère (tangente aux arêtes) : a Ö2 ; sphère circonscrite : a Ö3
Mensurations	volume : a3       aire : 6 a²    rapport volume/(volume de la sphère circonscrite) : 37% coefficient isopérimétrique :
Construction	Tétraèdre régulier augmenté de quatre pyramide dont les faces sont coplanaires avec les voisines :
Coordonnées  des sommets	avec ,  2 sommets étant reliés par une arête ss'ils ont deux coordonnées en commun. Équation cartésienne du cube plein : ,  donnant la réunion des faces.
Plans de symétrie	3 parallèles aux faces, 6 contenant des arêtes opposées
Axes de rotation	3 passant par les milieux de faces opposées (2 rotations d'ordre 4 et une d'ordre 2 par axe) 4 passant par des sommets opposés (2 rotations d'ordre 3  par axe) Remarquer cette vue hexagonale d'un cube ! 6 passant par les milieux d'arêtes opposées (1 rotation d'ordre 2  par axe)
Groupe des isométries	ordre 48 : 24 rotations (l'identité, 6 quarts de tour, 8 tiers de tour, 9 demi-tours)  et 24 antirotations (produits des précédentes par la symétrie de centre O, dont 9 réflexions) Le sous-groupe des 24 rotations est isomorphe à S4 (action simple et transitive sur les 4 diagonales).
Pavage	le cube est le seul polyèdre régulier pavant l'espace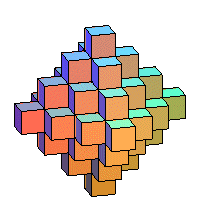
Polyèdres dérivés	par troncature forte : cuboctaèdre ; par troncature faible : cube tronqué ;  par chanfreinage : rhombicuboctaèdre ; par chanfreinage fort : cuboctaèdre tronqué ; par adoucissement : cube adouci ;  par augmentation : dodécaèdre régulier, dodécaèdre rhombique, tetraki-hexaèdre.
Avatar	le cube de Sierpinski.

Le cube est un tétraèdre tronqué aux arêtes

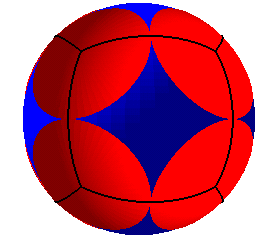
Bien que le cube soit un polyèdre régulier, il ne donne pas la réponse au problème des dictateurs ennemis dans le cas n = 8, problème demandant comment sont disposées sur une sphère n calottes sphériques identiques (les empires de chaque dicateur) de taille maximale et ne se chevauchant pas. La répartition fournie par les 8 calottes identiques maximales centrées au sommet d'un cube n'est pas optimale (on voit bien, figure supérieure, qu'il y a encore beaucoup de bleu !).  La réponse optimale est donnée par l'antiprisme à base carrée et faces régulières. Source : Marcel Berger, pour la Science 176, p. 72 et dossier Pour la Science 41 p. 40.

Ci-contre, vue du polyèdre composé formé du cube et de l'octaèdre dual polaire par rapport à la sphère tangente aux arêtes  ; la partie commune est le cuboctaèdre. L'enveloppe des sommets est le dodécaèdre rhombique.

Voir aussi l'hypercube.

Beau lien : mathematische-basteleien.de/cube.htm
 

Cristal cubique de fluorite.	Les pièces formant le ballon de foot classique suivent un icosaèdre tronqué, mais depuis la coupe du Monde 2014, on voit des ballons dont les pièces forment un ensemble homéomorphe au cube !	Réseau cubique tentaculaire dans "la fièvre d'Urbicande" de Schuiten et Peeters.

 

L'atomium de Bruxelles a une forme cubique. Mais le cube étant posé sur sa pointe, on voit un hexagone.

 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2023