Hypercube

HYPERCUBE
Hypercube, Hyperkubus

La notion d'hypercube est la généralisation à une dimension quelconque de celle de carré en dimension 2, ou de cube en dimension 3.

Définitions	polytope d'ordre n dont toutes les faces sont des carrés parallélotope rectangle d'ordre n à arêtes de même longueur
Définition par récurrence	un hypercube d'ordre 2 étant un carré, un hypercube d'ordre n est un polytope d'ordre n dont toutes les n – 1 cellules sont des hypercubes d'ordre n– 1
Autre nom	polytope de mesure (Coxeter)
Famille	polytope régulier
Symbole de Schläfli	{4, 3, ...., 3} (3 hyperfaces entourant chaque n–3-cellule, pour )
Dual	cocube de dimension n
(n -1) - cellules	2n hypercubes de dimension n -1
k - cellules	hypercubes de dimension k, appartenant chacun à q - cellules.
Arêtes	arêtes de longueur a, appartenant chacune à k-cellules.
Sommets	2ⁿ sommets, appartenant chacun à k - cellules.
Graphe des arêtes	graphe à 2ⁿ sommets régulier de degré n ; voir plus de précisions sur mathworld.
Diamètres	hypersphère inscrite : a ; hypersphère circonscrite : .
Mensurations	mesure n-dimensionnelle de l'hypercube plein : aⁿ mesure n-1-dimensionnelle de sa frontière :
Coordonnées des sommets	avec , ou avec x_i= 0 ou a ; pour obtenir les sommets d'une k-cellule, fixer n – k coordonnées et faire varier les k autres. 2 sommets sont donc dans une même k-cellule ss'ils ont au moins n – k coordonnées identiques.
Groupe des isométries	groupe d' ordre: ; voir cette page.

Programme Maple générant l'hypercube d'ordre n
(hypercube (4)[1,2] donne la deuxième face de la première cellule de l'hypercube de dimension 4 ) :
inserer:=proc(x,L,k,n)
if n=0 then [seq(L[q],q=1..k-1),x,seq(L[q],q=k..nops(L))]
else map(LL->inserer(x,LL,k,n-1),L) fi end:
hypercube:=proc(n)
local H:
if n =1 then {[0], [1]}
else H := hypercube(n-1):
{seq(inserer(0,H,k,n-1),k=1..n), seq(inserer(1,H,k,n-1),k=1..n)} fi end:

Son équivalent Mathematica :
inserer[x_, L_, k_, n_] :=
If[ n == 0, Insert[L, x, k],
Map[inserer[x, #, k, n - 1] &, L] ]

hypercube[n_] := Module[
{H},
If[ n == 1 , {{0}, {1}},
H = hypercube[n - 1];
Join[Table[inserer[0, H, k, n - 1], {k, 1, n}], Table[inserer[1, H, k, n - 1], {k, 1, n}]]]]

Voir page suivante le cas de l'hypercube de dimension 4.
Voir aussi les zonogones, zonoèdres, et zonotopes, projections 2D, 3D et nD d'un hypercube plein.

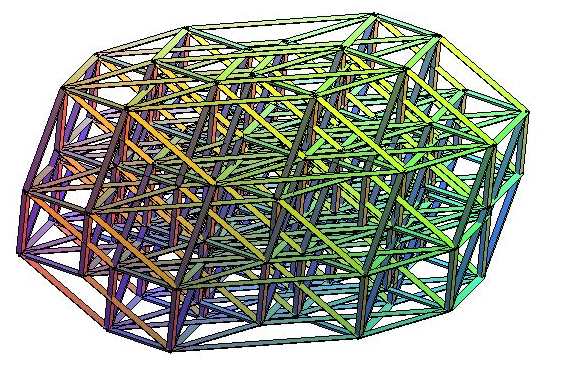
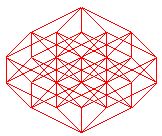
Ci-dessus, projection orthogonale 3D des arêtes de l'hypercube de dimension 7.

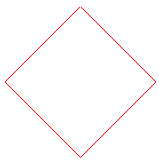
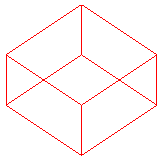
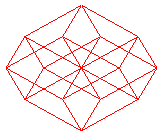
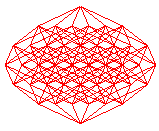
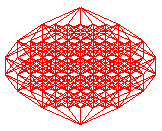
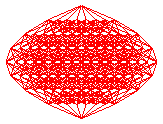
Ci-dessous, projections planes des divers hypercubes de dimension 2 à 9 ; les n arêtes issues d'un des sommets ont été projetées en les n vecteurs de même modules exp( i k pi /n) pour k allant de 0 à n-1.

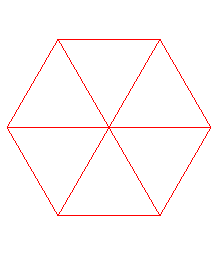
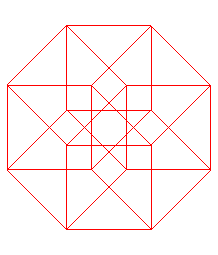
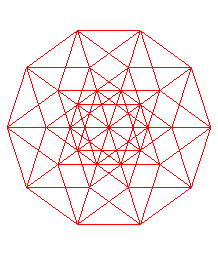
carré cube 4-hypercube 5-hypercube

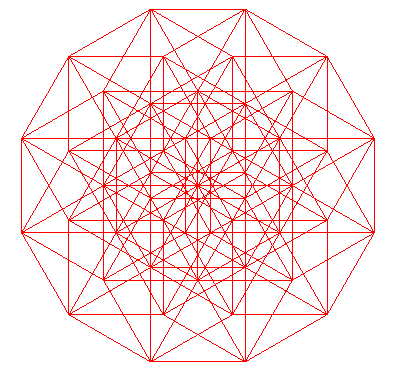
6-hypercube 7-hypercube
8-hypercube 9-hypercube

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres