4-Hypercube

HYPERCUBE DE DIMENSION 4 ou TESSERACT

Les images Povray de cette page ont été réalisées par Alain Esculier.

Coordonnées des sommets regroupés par arêtes :
[[-1,-1,-1,-1],[1,-1,-1,-1]],[[1,-1,-1,-1],[1,1,-1,-1]],[[1,1,-1,-1],[1,1,1,-1]],[[1,1,1,-1],[1,1,1,1]],[[1,1,-1,-1],[1,1,-1,1]],[[1,1,-1,1],[1,1,1,1]],[[1,-1,-1,-1],[1,-1,1,-1]],[[1,-1,1,-1],[1,1,1,-1]],[[1,-1,1,-1],[1,-1,1,1]],[[1,-1,1,1],[1,1,1,1]],
[[1,-1,-1,-1],[1,-1,-1,1]],[[1,-1,-1,1],[1,1,-1,1]],[[1,-1,-1,1],[1,-1,1,1]],[[-1,-1,-1,-1],[-1,1,-1,-1]],[[-1,1,-1,-1],[1,1,-1,-1]],[[-1,1,-1,-1],[-1,1,1,-1]],[[-1,1,1,-1],[1,1,1,-1]],[[-1,1,1,-1],[-1,1,1,1]],[[-1,1,1,1],[1,1,1,1]],
[[-1,1,-1,-1],[-1,1,-1,1]],[[-1,1,-1,1],[1,1,-1,1]],[[-1,1,-1,1],[-1,1,1,1]],[[-1,-1,-1,-1],[-1,-1,1,-1]],[[-1,-1,1,-1],[1,-1,1,-1]],[[-1,-1,1,-1],[-1,1,1,-1]],[[-1,-1,1,-1],[-1,-1,1,1]],[[-1,-1,1,1],[1,-1,1,1]],[[-1,-1,1,1],[-1,1,1,1]],
[[-1,-1,-1,-1],[-1,-1,-1,1]],[[-1,-1,-1,1],[1,-1,-1,1]],[[-1,-1,-1,1],[-1,1,-1,1]],[[-1,-1,-1,1],[-1,-1,1,1]]

Étymologie

tesseract (ou tessaract) : du grec tessares "quatre" ; ce nom a été donné par Charles Howard Hinton en 1888.

Autres noms

4-cube, 4-hypercube, 8 cellules, C₈, octachore, octatope.

Définitions

polychore (= 4-polytope) dont toutes les cellules sont des cubes ou dont toutes les faces sont des carrés,
parallélochore à arêtes de mêmes longueur

Famille

polychore régulier

Dual

hyperoctaèdre de dimension 4

Symbole de Schläfli

{4, 3, 3} (3 cubes autour de chaque arête)

Cellules

8 cubes

Faces

24 carrés

Arêtes

32 arêtes de longueur a appartenant chacune à 3 faces et à 3 cellules.

Sommets

16 sommets appartenant chacun à 4 arêtes, 6 faces, et 4 cellules.

Base de calotte

tétraèdre

Patron

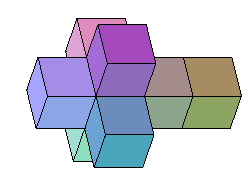(261 patrons en tout)

Graphe des arêtes

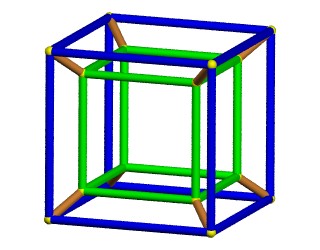
Voir diverses représentations planes de ce graphe à 16 sommets régulier de degré 4 sur mathworld.

Diamètres

hypersphère inscrite : a ; hypersphère circonscrite : 2a

Mensurations

hypervolume de l'hypercube plein : a⁴ volume de sa frontière : 8 a³

Coordonnées
des sommets

avec

, ou

avec x_i= 0 ou a.

pour obtenir une

cellule
face
arête

on fixe

une
deux
trois

coordonnée(s) et on fait varier l(es)

trois
deux
une

autre(s)

2 sommets sont donc reliés par une arête ss'ils ne diffèrent que d'une coordonnée ;
ils sont dans une même face ss'ils ont au moins deux coordonnées identiques
et sont dans une même cellule ss'ils ont au moins une coordonnée identique.

Groupe des isométries

ordre 384 = 2⁷.3 = 2⁴.4!

Pavage

Comme ses analogues en toutes dimensions, le 4-hypercube pave l'espace, mais contrairement à la dimension 3 où le cube est le seul polyèdre régulier à paver l'espace, en dimension 4, il est accompagné par l'hyperoctaèdre et l'hypergranatoèdre.

Sites

fr.wikipedia.org/wiki/Hypercube
eusebeia.dyndns.org/4d/8-cell.html
www.polytope.de/c8.html
mathematische-basteleien.de/hypercube.htm

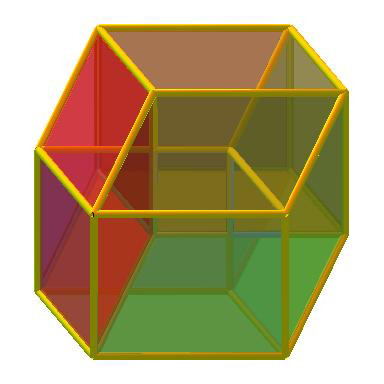
Projection affine de l'hypercube 4D avec indication des huit cellules.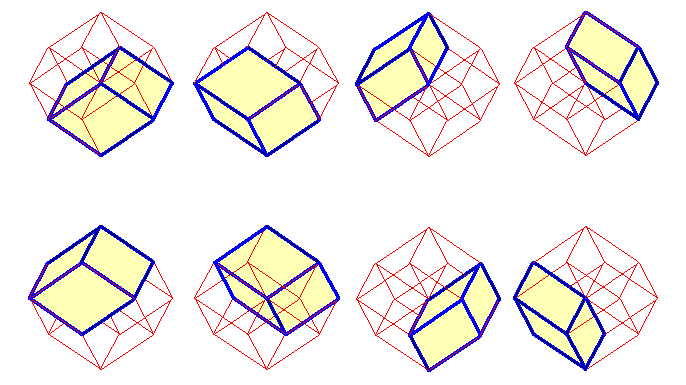

Un segment translaté donne un carré, qui translaté donne un cube, qui translaté donne un hypercube 4D etc....

Les coordonnées des sommets d'un hypercube 4D de diagonale [(0,0,0,0) (1,1,1,1)] écrites sans parenthèses donnent les entiers de 0 à 15 écrits en binaire. Ceci permet un codage simple de ces sommets.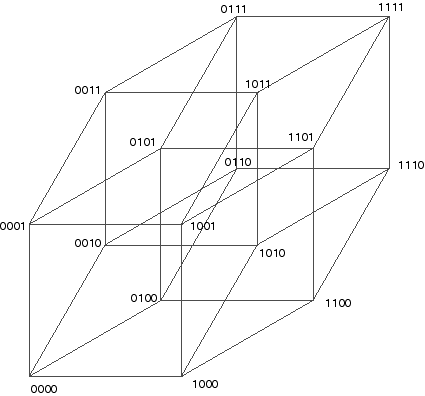

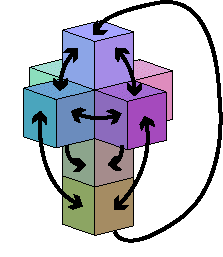
Ci-contre une figure montrant quelles faces se recollent entre elles lorsqu'on passe du patron à l'hypercube. Ceci s'effectue par des rotations autour de faces de chaque cube en dimension 4.

Au milieu, le célèbre tableau de Dali (1954) "crucifixion" sous-titré "Corpus Hypercubus" où la croix est remplacée par un patron d'hypercube.

A droite, mosaïque de Luigi La Ferla " L' APPARENCE DE LA LUMIÈRE 2022".

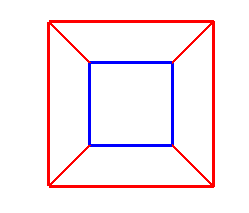
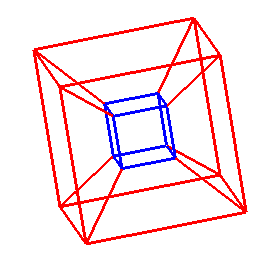
De même que la perspective (c'est-à-dire la perspective conique plane) d'un cube vu de face donne la figure ci-contre à gauche, la perspective conique d'un hypercube 4D sur un hyperplan parallèle à une cellule, elle même projetée (affinement cette fois) sur un plan, donne la figure de droite.
On remarquera que de même que la perpective du cube ne donne que 5 faces apparentes (la sixième recouvre les autres), la perspective de l'hypercube ne donne que 7 cellules apparentes (la huitième englobe les autres).

Un projection conique inhabituelle de l'hypercube, en tétraèdre régulier : 4 des huit cubes se projettent en des hexaèdres et les 4 autres dégénèrent en des tétraèdres. L'observateur est placé en un sommet de l'hypercube et le regarde suivant une diagonale.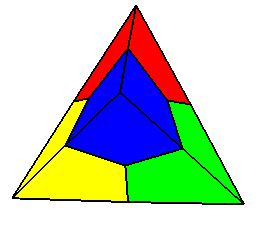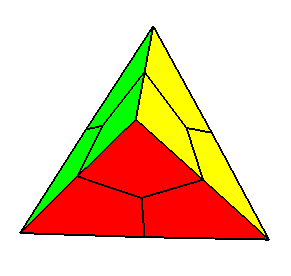

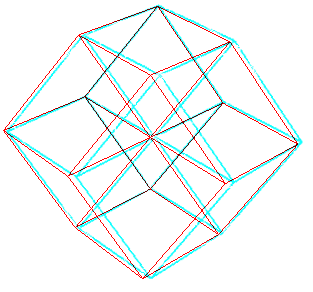
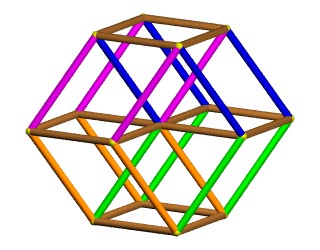
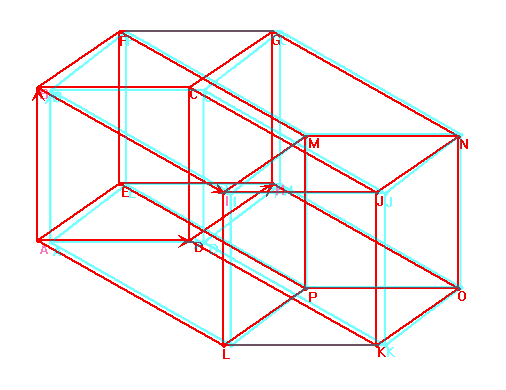
De la même façon qu'un cube plein se projette orthogonalement sur le plan orthogonal à une grande diagonale en un hexagone régulier plein, un hypercube 4D plein se projette sur l'hyperplan orthogonal à une grande diagonale en un dodécaèdre rhombique plein.
Dans l'anaglyphe ci-contre, à regarder avec des lunettes rouge (à gauche) et bleu (à droite)

, on essaiera de distinguer les 8 parallélépipèdes projetés des 8 cellules cubiques de l'hypercube.
Voir aussi ce site : dogfeathers.com/mark/rhdodec.html

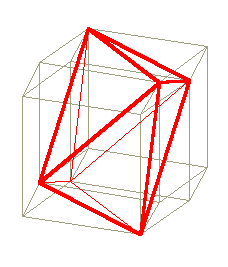La section d'un hypercube 4D par un hyperplan orthogonal à une grande diagonale, et passant par le centre, est un octaèdre régulier.

La section d'un hypercube 4D par l'hyperplan contenant les quatre sommets voisins d'un sommet donné est, elle, un tétraèdre régulier.

Un hypercube est en rotation autour d'un plan (oui, d'un plan...) ; cet hypercube est projeté orthogonalement sur un hyperplan (donc un espace de dimension 3), et cette image est projetée sur le plan de votre écran :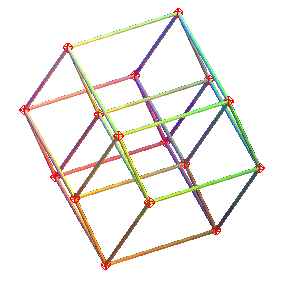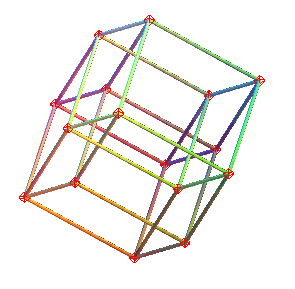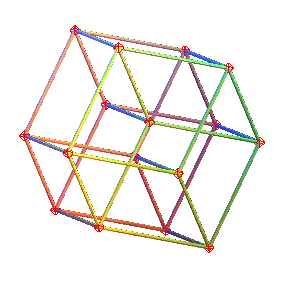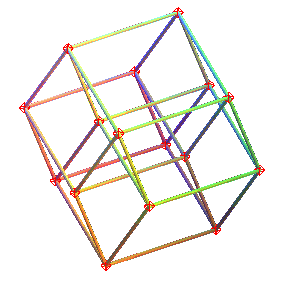

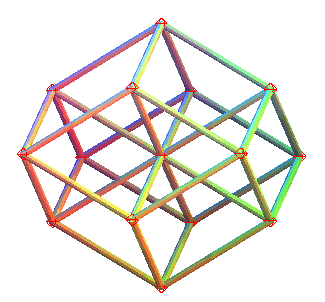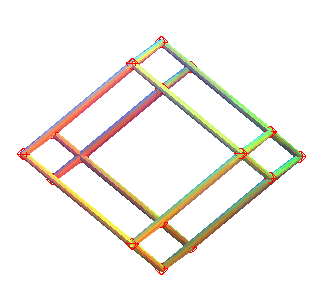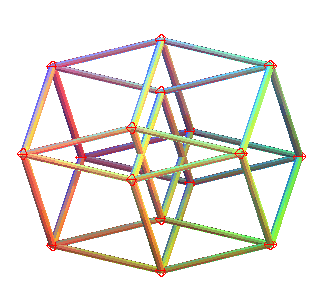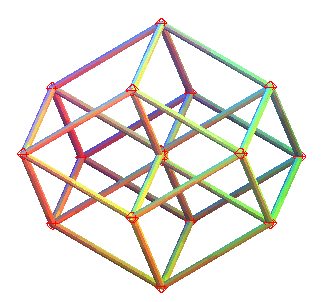Anaglyphe d'une projection affine tridimensionnelle du squelette de l'hypercube, à regarder avec des lunettes rouge (à gauche) et bleu (à droite)

Projection affine plane avec passages "dessus" pour les arêtes les plus proches (logo de la start-up hypercube): essayer de voir les huit cellules, 3 par arêtes.

L'architecte de la grande arche de la Défense a-t-il pensé à l'hypercube en la concevant ?

"Ipercubo", sculpture d'Attilio Pierelli.

Des boucles d'oreilles avec patron d'hypercube

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres