HYPERGRANATOÈDRE
24-cell, 24-Zell
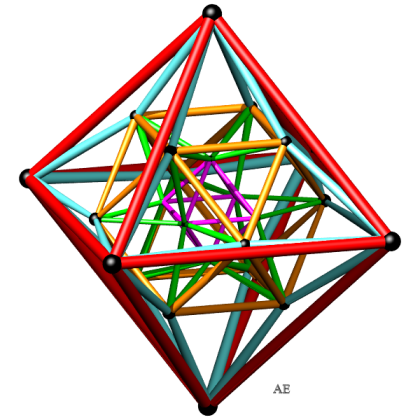
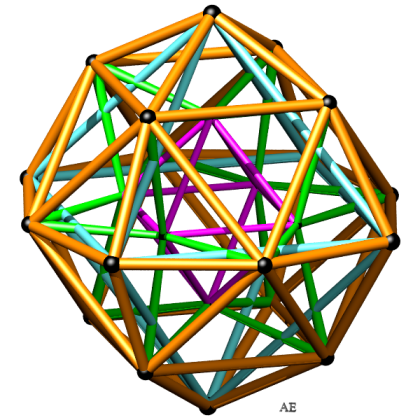
Projections conique dans R3 : les arêtes sont coloriées
suivant leur distance au centre.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
HYPERGRANATOÈDRE
24-cell, 24-Zell


Projections conique dans R3 : les arêtes sont coloriées
suivant leur distance au centre.
| Origine du nom | de hyper et granatoèdre, autre nom du dodécaèdre rhombique (à cause de leurs constructions similaires) |
| Autres noms | C24, 24 cellules, icositétrachore, icositétratope (de icosi "20" et tétra "4"), polyoctaèdre, octaplexe (= complexe d'octaèdres) |
| Famille | polychore régulier |
| Dual | lui-même |
| Symbole de Schläfli | {3, 4, 3} (3 cellules octaédriques autour de chaque arête) |
| Cellules | 24 octaèdres |
| Faces | 96 triangles |
| Arêtes | 96 arêtes de longueur a communes chacune à 3 faces et 3 cellules |
| Sommets | 24 sommets ; à chaque sommet aboutissent 8 arêtes, 12 triangles et 6 octaèdres |
| Base de calotte | cube |
| Patrons | environ 1,8. 1016 patrons différents en tout |
| Graphe des arêtes | graphe à 24 sommets régulier de degré 8 ; voir ici des renseignements supplémentaires |
| Diamètres | hypersphère inscrite : 2a ; hypersphère circonscrite : 2a |
| Mensurations | hypervolume : |
| Construction | augmentation d'un 4-hypercube
(coller huit hyperpyramides
à base cubiques sur les huit cellules de l'hypercube)
troncature d'un 4-hyperoctaèdre (les sommets de l'hypergranatoèdre sont les milieux des 24 arêtes de l'hyperoctaèdre). |
| Coordonnées
des sommets, arêtes, faces, cellules en dimension 4 |
(±1, ±1, 0, 0) et permutés pour une longueur d'arête a = Deux sommets sont extrémités de la même arête ss'ils ont exactement deux coordonnées en commun, par exemple : (1,1,0,0) et (1,0,1,0) ; ci-dessous, la liste des arêtes, regroupées en 24 carrés disjoints : [[[-1,0,-1,0],[-1,-1,0,0],[0,-1,0,1],[0,0,-1,1],[-1,0,-1,0]], [[-1,0,-1,0],[-1,0,0,-1],[-1,0,1,0],[-1,0,0,1],[-1,0,-1,0]], [[-1,0,-1,0],[0,0,-1,-1],[0,1,0,-1],[-1,1,0,0],[-1,0,-1,0]], [[-1,0,0,1],[-1,-1,0,0],[0,-1,1,0],[0,0,1,1],[-1,0,0,1]], [[0,-1,-1,0],[0,-1,0,-1],[0,-1,1,0],[0,-1,0,1],[0,-1,-1,0]], [[0,-1,-1,0],[0,0,-1,-1],[-1,0,0,-1],[-1,-1,0,0],[0,-1,-1,0]], [[0,-1,-1,0],[1,-1,0,0],[1,0,0,1],[0,0,-1,1],[0,-1,-1,0]], [[0,-1,0,-1],[0,0,1,-1],[-1,0,1,0],[-1,-1,0,0],[0,-1,0,-1]], [[0,-1,0,-1],[1,0,0,-1],[0,1,0,-1],[-1,0,0,-1],[0,-1,0,-1]], [[0,1,-1,0],[-1,1,0,0],[-1,0,0,1],[0,0,-1,1],[0,1,-1,0]], [[0,1,-1,0],[0,0,-1,-1],[1,0,0,-1],[1,1,0,0],[0,1,-1,0]], [[0,1,-1,0],[0,1,0,-1],[0,1,1,0],[0,1,0,1],[0,1,-1,0]], [[0,1,1,0],[-1,1,0,0],[-1,0,0,-1],[0,0,1,-1],[0,1,1,0]], [[0,1,0,1],[-1,1,0,0],[-1,0,1,0],[0,0,1,1],[0,1,0,1]], [[1,-1,0,0],[1,0,0,-1],[0,0,1,-1],[0,-1,1,0],[1,-1,0,0]], [[1,-1,0,0],[1,0,1,0],[0,0,1,1],[0,-1,0,1],[1,-1,0,0]], [[1,0,0,1],[0,1,0,1],[-1,0,0,1],[0,-1,0,1],[1,0,0,1]], [[1,0,0,1],[1,1,0,0],[0,1,1,0],[0,0,1,1],[1,0,0,1]], [[1,0,-1,0],[0,0,-1,-1],[0,-1,0,-1],[1,-1,0,0],[1,0,-1,0]], [[1,0,-1,0],[0,1,-1,0],[-1,0,-1,0],[0,-1,-1,0],[1,0,-1,0]], [[1,0,-1,0],[1,0,0,-1],[1,0,1,0],[1,0,0,1],[1,0,-1,0]], [[1,0,-1,0],[1,1,0,0],[0,1,0,1],[0,0,-1,1],[1,0,-1,0]], [[1,0,1,0],[0,1,1,0],[-1,0,1,0],[0,-1,1,0],[1,0,1,0]], [[1,0,1,0],[1,1,0,0],[0,1,0,-1],[0,0,1,-1],[1,0,1,0]]] Trois sommets s'ils sont du type ( a,b,0,0 ),( a,0,c,0) et (a,0,0,d) ou (0,a,b,0), (0,0,b,c) et (0,a,0,c), avec a,b,c égaux à +-1, avec permutations possibles (noter qu'il y a deux coordonnées identiques) |
| Autres coordonnées possibles (celles du dual en fait) | (±2, 0, 0, 0) et permutés (8 sommets d'un
hyperoctaèdre)
et (±1, ±1, ±1, ±1) (16 sommets d'un hypercube) pour une longueur d'arête a = 2 ; ci-dessous, la liste des 96 arêtes : [[[-2, 0, 0, 0], [-1, -1, -1, -1]], [[-2, 0, 0, 0], [-1, -1, -1, 1]], [[-2, 0, 0, 0], [-1, -1, 1, -1]], [[-2, 0, 0, 0], [-1, -1, 1, 1]], [[-2, 0, 0, 0], [-1, 1, -1, -1]], [[-2, 0, 0, 0], [-1, 1, -1, 1]], [[-2, 0, 0, 0], [-1, 1, 1, -1]], [[-2, 0, 0, 0], [-1, 1, 1, 1]], [[2, 0, 0, 0], [1, -1, -1, -1]], [[2, 0, 0, 0], [1, -1, -1, 1]], [[2, 0, 0, 0], [1, -1, 1, -1]], [[2, 0, 0, 0], [1, -1, 1, 1]], [[2, 0, 0, 0], [1, 1, -1, -1]], [[2, 0, 0, 0], [1, 1, -1, 1]], [[2, 0, 0, 0], [1, 1, 1, -1]], [[2, 0, 0, 0], [1, 1, 1, 1]], [[0, -2, 0, 0], [-1, -1, -1, -1]], [[0, -2, 0, 0], [-1, -1, -1, 1]], [[0, -2, 0, 0], [-1, -1, 1, -1]], [[0, -2, 0, 0], [-1, -1, 1, 1]], [[0, -2, 0, 0], [1, -1, -1, -1]], [[0, -2, 0, 0], [1, -1, -1, 1]], [[0, -2, 0, 0], [1, -1, 1, -1]], [[0, -2, 0, 0], [1, -1, 1, 1]], [[0, 2, 0, 0], [-1, 1, -1, -1]], [[0, 2, 0, 0], [-1, 1, -1, 1]], [[0, 2, 0, 0], [-1, 1, 1, -1]], [[0, 2, 0, 0], [-1, 1, 1, 1]], [[0, 2, 0, 0], [1, 1, -1, -1]], [[0, 2, 0, 0], [1, 1, -1, 1]], [[0, 2, 0, 0], [1, 1, 1, -1]], [[0, 2, 0, 0], [1, 1, 1, 1]], [[0, 0, -2, 0], [-1, -1, -1, -1]], [[0, 0, -2, 0], [-1, -1, -1, 1]], [[0, 0, -2, 0], [-1, 1, -1, -1]], [[0, 0, -2, 0], [-1, 1, -1, 1]], [[0, 0, -2, 0], [1, -1, -1, -1]], [[0, 0, -2, 0], [1, -1, -1, 1]], [[0, 0, -2, 0], [1, 1, -1, -1]], [[0, 0, -2, 0], [1, 1, -1, 1]], [[0, 0, 2, 0], [-1, -1, 1, -1]], [[0, 0, 2, 0], [-1, -1, 1, 1]], [[0, 0, 2, 0], [-1, 1, 1, -1]], [[0, 0, 2, 0], [-1, 1, 1, 1]], [[0, 0, 2, 0], [1, -1, 1, -1]], [[0, 0, 2, 0], [1, -1, 1, 1]], [[0, 0, 2, 0], [1, 1, 1, -1]], [[0, 0, 2, 0], [1, 1, 1, 1]], [[0, 0, 0, -2], [-1, -1, -1, -1]], [[0, 0, 0, -2], [-1, -1, 1, -1]], [[0, 0, 0, -2], [-1, 1, -1, -1]], [[0, 0, 0, -2], [-1, 1, 1, -1]], [[0, 0, 0, -2], [1, -1, -1, -1]], [[0, 0, 0, -2], [1, -1, 1, -1]], [[0, 0, 0, -2], [1, 1, -1, -1]], [[0, 0, 0, -2], [1, 1, 1, -1]], [[0, 0, 0, 2], [-1, -1, -1, 1]], [[0, 0, 0, 2], [-1, -1, 1, 1]], [[0, 0, 0, 2], [-1, 1, -1, 1]], [[0, 0, 0, 2], [-1, 1, 1, 1]], [[0, 0, 0, 2], [1, -1, -1, 1]], [[0, 0, 0, 2], [1, -1, 1, 1]], [[0, 0, 0, 2], [1, 1, -1, 1]], [[0, 0, 0, 2], [1, 1, 1, 1]], [[-1, -1, -1, -1], [-1, -1, -1, 1]], [[-1, -1, -1, -1], [-1, -1, 1, -1]], [[-1, -1, -1, -1], [-1, 1, -1, -1]], [[-1, -1, -1, -1], [1, -1, -1, -1]], [[-1, -1, -1, 1], [-1, -1, 1, 1]], [[-1, -1, -1, 1], [-1, 1, -1, 1]], [[-1, -1, -1, 1], [1, -1, -1, 1]], [[-1, -1, 1, -1], [-1, -1, 1, 1]], [[-1, -1, 1, -1], [-1, 1, 1, -1]], [[-1, -1, 1, -1], [1, -1, 1, -1]], [[-1, -1, 1, 1], [-1, 1, 1, 1]], [[-1, -1, 1, 1], [1, -1, 1, 1]], [[-1, 1, -1, -1], [-1, 1, -1, 1]], [[-1, 1, -1, -1], [-1, 1, 1, -1]], [[-1, 1, -1, -1], [1, 1, -1, -1]], [[-1, 1, -1, 1], [-1, 1, 1, 1]], [[-1, 1, -1, 1], [1, 1, -1, 1]], [[-1, 1, 1, -1], [-1, 1, 1, 1]], [[-1, 1, 1, -1], [1, 1, 1, -1]], [[-1, 1, 1, 1], [1, 1, 1, 1]], [[1, -1, -1, -1], [1, -1, -1, 1]], [[1, -1, -1, -1], [1, -1, 1, -1]], [[1, -1, -1, -1], [1, 1, -1, -1]], [[1, -1, -1, 1], [1, -1, 1, 1]], [[1, -1, -1, 1], [1, 1, -1, 1]], [[1, -1, 1, -1], [1, -1, 1, 1]], [[1, -1, 1, -1], [1, 1, 1, -1]], [[1, -1, 1, 1], [1, 1, 1, 1]], [[1, 1, -1, -1], [1, 1, -1, 1]], [[1, 1, -1, -1], [1, 1, 1, -1]], [[1, 1, -1, 1], [1, 1, 1, 1]], [[1, 1, 1, -1], [1, 1, 1, 1]]] |
| Coordonnées des sommets d'une projection conique en dimension 3 (utilisée pour la vue ci-dessus) | (±a,±a,0) et permutés, (±b,0,0)
et permutés, (±c,0,0) et permutés ; ci-dessous,
la liste arêtes regroupées en 24 carrés :
[[[a, 0., a], [a, a, 0.], [0., b, 0.], [0., 0., b], [a, 0., a]], [[a, 0., a], [c, 0., 0.], [a, 0., -a], [b, 0., 0.], [a, 0., a]], [[a, 0., a], [0., 0., c], [0., -c, 0.], [a, -a, 0.], [a, 0., a]], [[b, 0., 0.], [a, a, 0.], [0., a, -a], [0., 0., -a], [b, 0., 0.]], [[0., a, a], [0., c, 0.], [0., a, -a], [0., b, 0.], [0., a, a]], [[0., a, a], [0., 0., c], [c, 0., 0.], [a, a, 0.], [0., a, a]], [[0., a, a], [-a, a, 0.], [-a, 0., 0.], [0., 0., b], [0., a, a]], [[0., c, 0.], [0., 0., -c], [a, 0., -a], [a, a, 0.], [0., c, 0.]], [[0., c, 0.], [-c, 0., 0.], [0., -c, 0.], [c, 0., 0.], [0., c, 0.]], [[0., -a, a], [a, -a, 0.], [b, 0., 0.], [0., 0., b], [0., -a, a]], [[0., -a, a], [0., 0., c], [-c, 0., 0.], [-a, -a, 0.], [0., -a, a]], [[0., -a, a], [0., -c, 0.], [0., -a, -a], [0., -a, 0.], [0., -a, a]], [[0., -a, -a], [a, -a, 0.], [c, 0., 0.], [0., 0., -c], [0., -a, -a]], [[0., -a, 0.], [a, -a, 0.], [a, 0., -a], [0., 0., -a], [0., -a, 0.]], [[-a, a, 0.], [-c, 0., 0.], [0., 0., -c], [0., a, -a], [-a, a, 0.]], [[-a, a, 0.], [-a, 0., -a], [0., 0., -a], [0., b, 0.], [-a, a, 0.]], [[-a, 0., 0.], [0., -a, 0.], [b, 0., 0.], [0., b, 0.], [-a, 0., 0.]], [[-a, 0., 0.], [-a, -a, 0.], [0., -a, -a], [0., 0., -a], [-a, 0., 0.]], [[-a, 0., a], [0., 0., c], [0., c, 0.], [-a, a, 0.], [-a, 0., a]], [[-a, 0., a], [0., -a, a], [a, 0., a], [0., a, a], [-a, 0., a]], [[-a, 0., a], [-c, 0., 0.], [-a, 0., -a], [-a, 0., 0.], [-a, 0., a]], [[-a, 0., a], [-a, -a, 0.], [0., -a, 0.], [0., 0., b], [-a, 0., a]], [[-a, 0., -a], [0., -a, -a], [a, 0., -a], [0., a, -a], [-a, 0., -a]], [[-a, 0., -a], [-a, -a, 0.], [0., -c, 0.], [0., 0., -c], [-a, 0., -a]]] |
| Groupe des isométries | d'ordre 2.242 = 1152, dont la symétrie centrale. |
| Remarques : | pave l'espace
de dimension 4, comme l'hypercube et l'hyperoctaèdre (considérer
un pavage d'hypercubes et former dans un hypercube sur 2 les 8 hyperpyramides
de base une cellule et de sommet le centre de l'hypercube, et les accoler
aux hypercubes contigus afin de former des hypergranatoèdres)
seul polytope régulier autodual ayant un centre de symétrie |
| Sites | fr.wikipedia.org/wiki/Icositétrachore
http://mathworld.wolfram.com/24-Cell.html www.polytope.de/c24.html www.bathsheba.com/math/24cell/index.html en.wikipedia.org/wiki/Octacube_(mathematics) Voir aussi : Pour la Science, mars 2006 p. 96 |
Les sommets de l'hypergranatoèdre sont les centres
des 24 faces d'un hypercube
; les arêtes de l'hypergranatoèdre sont alors les 96 = 8.12
arêtes des 8 octaèdres déterminés par les milieux
des faces des 8 cellules de l'hypercube.
|
Gravure réalisée par Patrice Jeener, avec son aimable autorisation. |
 |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2018