ICOSAÈDRE
Icosahedron, Ikosaeder
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ICOSAÈDRE
Icosahedron, Ikosaeder

| Du grec "Ikosa" vingt, et "edros" siège,
base.
Vues Povray de cette page réalisées par Alain Esculier. Lien : mathematische-basteleien.de/ikosaeder.htm |
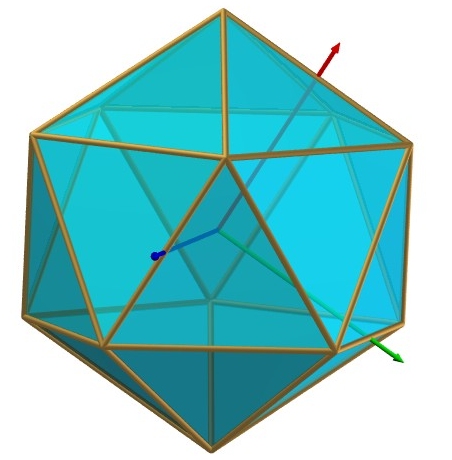
Un icosaèdre est un polyèdre à vingt faces.
Le plus célèbre est l'icosaèdre régulier
dont voici la carte de visite :
| Famille | polyèdre régulier, et aussi antidiamant. | ||||||
| Historique | solide connu de Platon en 370 av. J.C. | ||||||
| Dual | dodécaèdre
régulier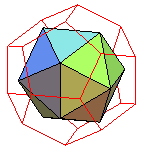 ¬
dual
polaire de l'icosaèdre par rapport à sa sphère circonscrite ¬
dual
polaire de l'icosaèdre par rapport à sa sphère circonscrite |
||||||
| Faces | 20 triangles | ||||||
| Sommets | 12 sommets de degré 5, de code de Schläfli 35 | ||||||
| Arêtes | 30 arêtes de longueur a ; angle dièdre
: |
||||||
| Patrons |
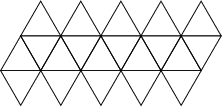 Il
y en a 43380 en tout (comme pour le dodécaèdre) Il
y en a 43380 en tout (comme pour le dodécaèdre) |
||||||
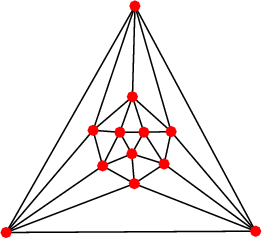
| Graphe des
arêtes :
graphe icosaédrique |
 |
||||||
| Diamètres | sphère inscrite : où |
||||||
| Mensurations | volume : coefficient isopérimétrique : (meilleur coefficient isopérimétrique des polyèdres réguliers) |
||||||
| Coordonnées
des 12 sommets (voir le repère dans la première vue ci-dessus) |
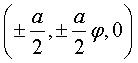 permutés circulairement,
permutés circulairement,
2 sommets étant reliés par une arête ssi leur distance vaut a. |
||||||
| Équations des 20 plans faces | 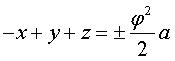 et
ses 3 permutés, et
ses 3 permutés, |
||||||
| Équation de la surface | |||||||
| Constructions | 1) à partir de 3 rectangles d'or (rapport longueur/largeur
égal au nombre d'or) 2 à 2 orthogonaux
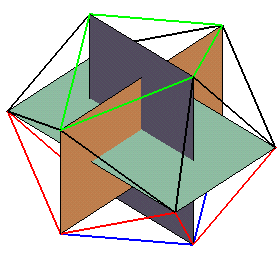 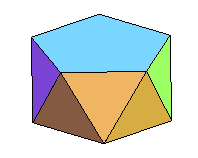 + +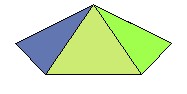 + +
3) par adoucissement du tétraèdre. 4) Par troncature d'un octaèdre (voir ci-dessous) 5) par la méthode de Buckminster (voir ci-dessous) |
||||||
| Plans de symétrie | les 15 plans contenant deux arêtes opposées | ||||||
Axes de rotation
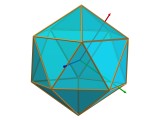 |
|
||||||
| Groupe des isométries | ordre 120 : 60 rotations (l'identité, 12
cinquièmes de tours, 12 deux cinquièmes de tours, 20 tiers
de tours, 15 demi-tours) et 60 antirotations
(produits
des précédentes par la symétrie de centre
O,
dont 15 réflexions)
Le sous-groupe des 60 rotations est isomorphe au groupe A5 des permutations paires de 5 objets (action sur un ensemble de 5 tétraèdres réguliers inscrits). |
||||||
| Polyèdres dérivés | troncature forte
: icosidodécaèdre
; troncature faible : icosaèdre
tronqué ; adoucissement
:
dodécaèdre
adouci ; facettage : icosidodécaèdre
tronqué ; augmentation
: triaki-icosaèdre,
triacontaèdre
rhombique, hexaki-icosaèdre
Trois polyèdres réguliers étoilés ont les mêmes sommets que l'icosaèdre : le petit dodécaèdre étoilé, le grand dodécaèdre et le grand icosaèdre. Voir aussi les dômes géodésiques, l'hypericosaèdre et un bel icosaèdre arrondi comme surface de Goursat. |
| Si l'on effectue la construction par les trois rectangles
2 à 2 orthogonaux avec des rectangles quelconques, on obtient successivement
l'octaèdre, l'icosaèdre, et le cuboctaèdre.
Hochet utilisant cette construction. |
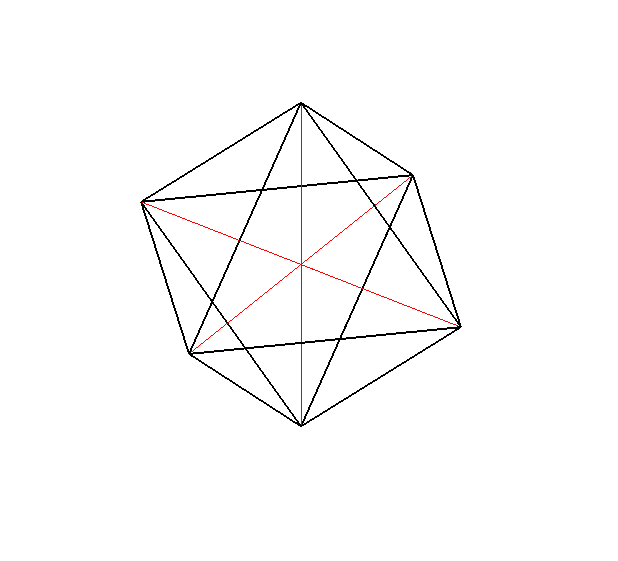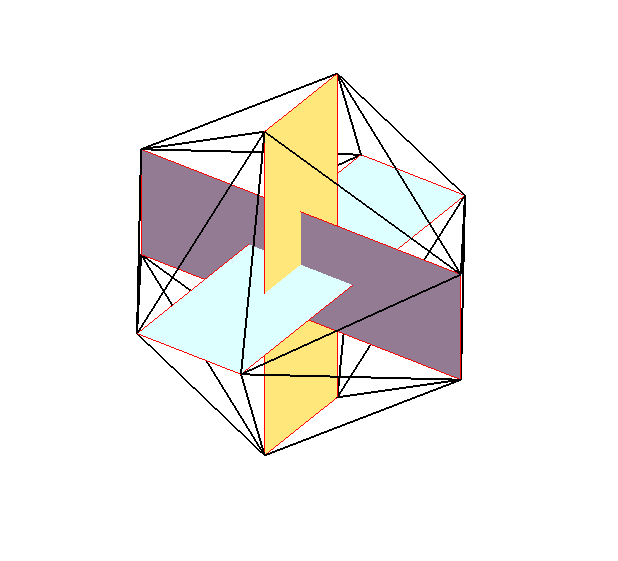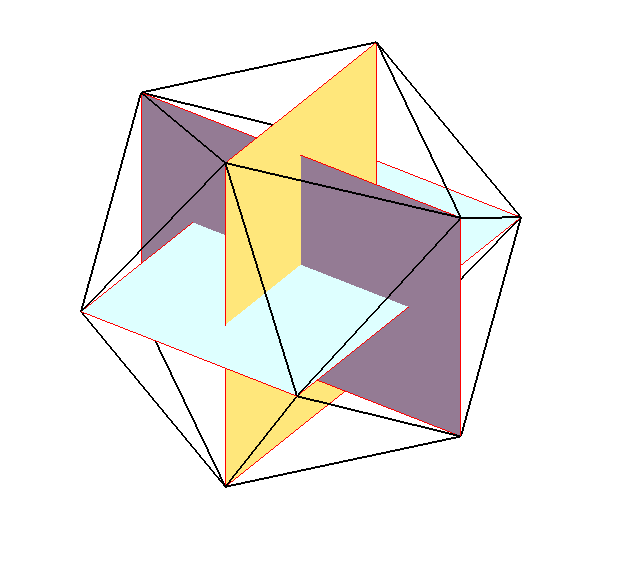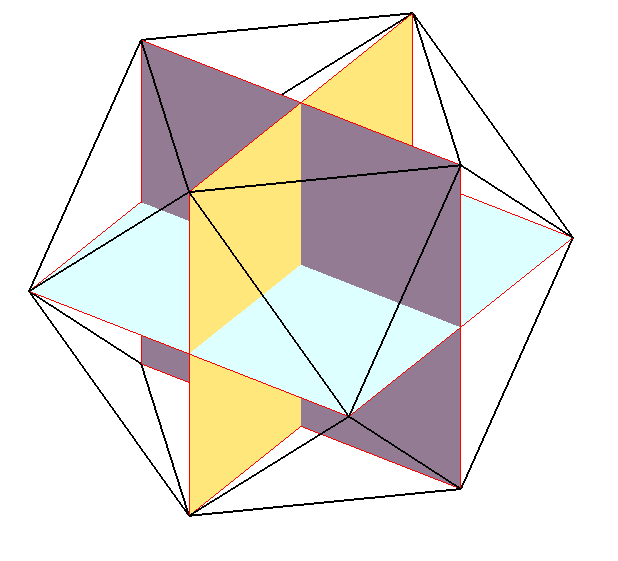 |
 |
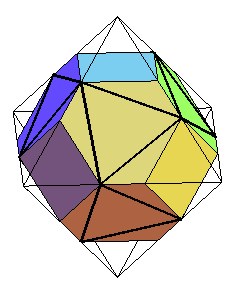 |
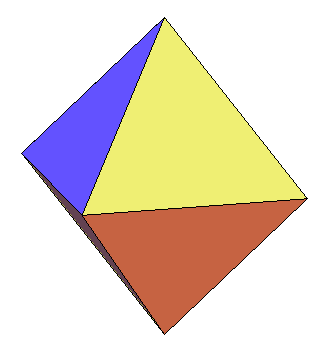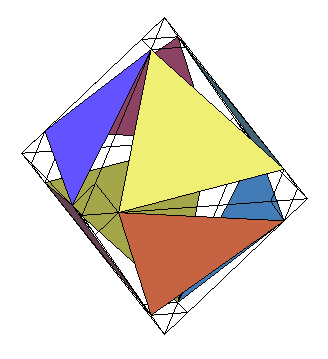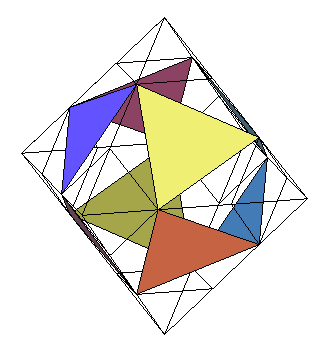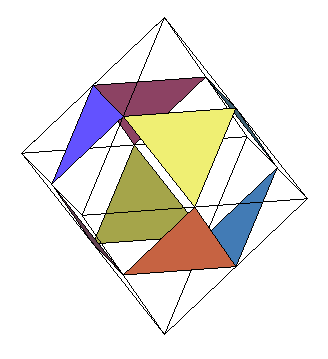
Lorsque l'on tronque progressivement les sommets d'un
octaèdre, on fait apparaître 8 faces hexagonales irrégulières
; mais si l'on prend un sommet sur deux sur ces faces, on obtient un assemblage
de 8 triangles équilatéraux, que l'on peut compléter
par 12 triangles isocèles (2 par sommet de l'octaèdre). Il
existe un moment où ces triangles isocèles sont équilatéraux,
ce qui donne alors l'icosaèdre régulier.
Attention, à ce moment l'octaèdre "tronqué" n'est pas l'"octaèdre tronqué" semi-régulier. |
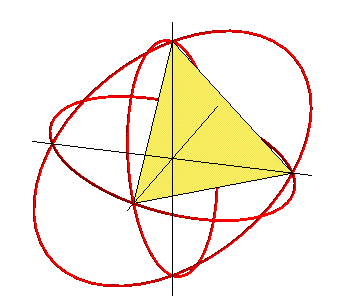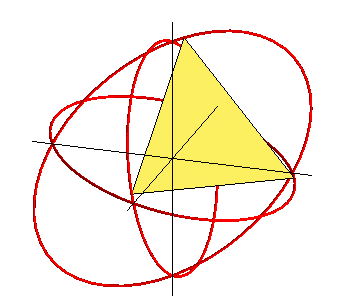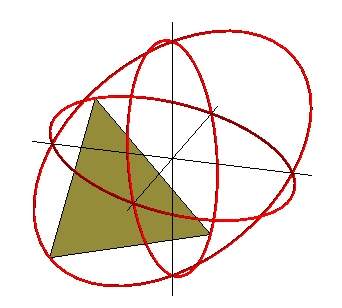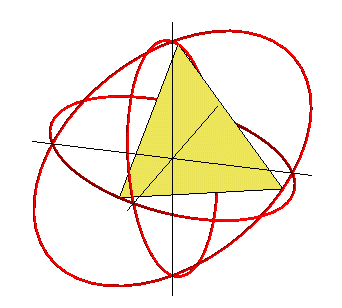 |
La construction suivante de l'icosaèdre a été
découverte par Richard
Buckminster Fuller ; si un triangle équilatéral de côté
fixé et d'axe de symétrie d'ordre 3 la droite x = y =
z est contraint d'avoir ses 3 sommets dans les 3 plans de coordonnées,
ses sommets décrivent des ellipses (celle du plan xOy est
définie par |
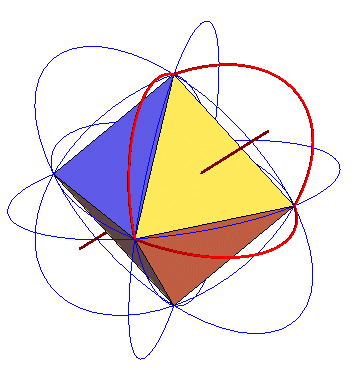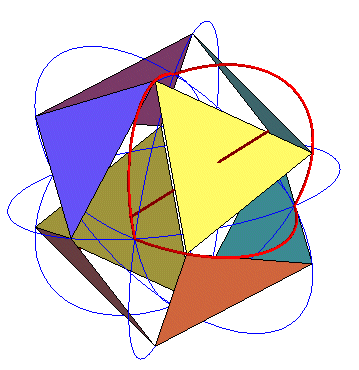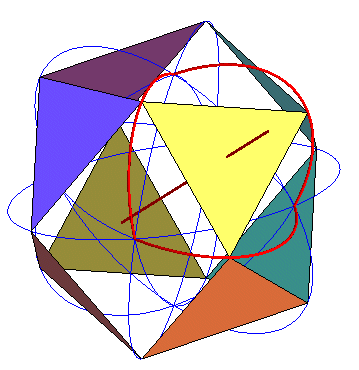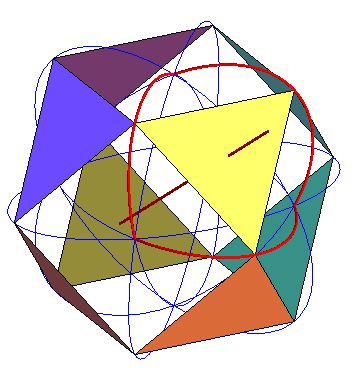 |
... Et si l'on effectue toutes les symétries de ce triangle par rapport aux plans de coordonnées, on obtient 8 triangles qui ont 3 positions remarquables ; l'une correspond à l'octaèdre, une deuxième au cuboctaèdre, et entre les deux, lorsque les ouvertures créées sont formées de deux triangles équilatéraux identiques au précédent, on obtient l'icosaèdre régulier... |
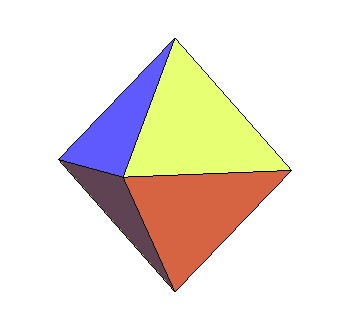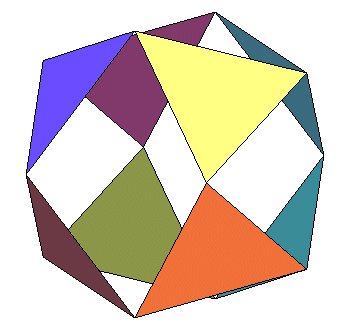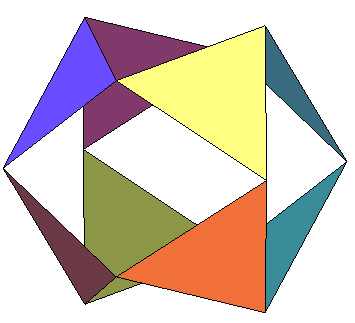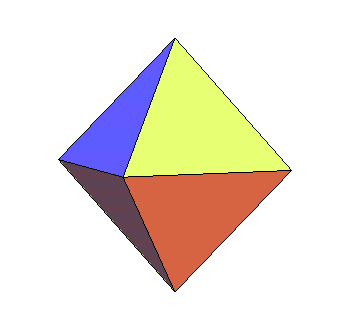 |
...Le mouvement a été baptisé par
Buckminster "jitterbug",
nom d'une danse.
Voir aussi cette vidéo et ce texte. Cette construction de l'icosaèdre est en fait, à homothétie près, la même que la précédente, ainsi que de l'antéprécédente. |
 |
Si l'on remplace les 20 sommets de coordonnées 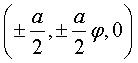 par ceux de coordonnées
par ceux de coordonnées |
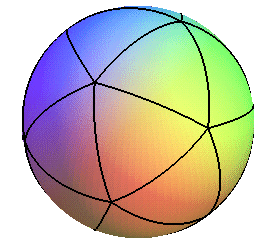 |
Projection centrale du squelette de l'icosaèdre sur la sphère circonscrite : on obtient un pavage régulier de la sphère par 20 triangles sphériques équilatéraux ; L'icosaèdre étant le polyèdre régulier ayant le maximum de faces, ce nombre de triangles équilatéraux est le plus grand possible. |
 |
Le problème dit "de la treizième sphère",
ou "du nombre d'embrassades" (kissing number).
Le rapport |
  |
Par projection, ce problème est équivalent à celui consistant à placer sur une sphère un nombre maximal de calottes sphériques d'angle au centre 60°. Le maximum est douze, mais on voit bien sur la figure ci-contre que la solution icosaédrique n'est pas unique. Sources : Ian Stewart, Pour la Science 174, p. 102. et Marcel Berger, dossier Pour la Science 41 p. 68. Le ballon de foot ci-contre a-t-il été réalisé
en liaison avec ce problème ?
|
 |
L'icosaèdre donne également une réponse
au problème dit "des dictateurs ennemis" dans le cas n =
12 : quel est la taille maximale de n calottes sphériques
identiques (les états de chaque dictateur) de sorte qu'elles puissent
se répartir sur une sphère sans se chevaucher, et quelle
est alors leur disposition ?
Réponse : les 12 calottes maximales ont un angle au centre de Sources : Marcel Berger, pour la Science 176, p. 72 et dossier Pour la Science 41 p. 40. |
| Ci-contre, polyèdre composé formé de l'icosaèdre et du dodécaèdre dual polaire par rapport à la sphère tangente aux arêtes ; la partie commune est l'icosidodécaèdre. |  |
 |
 |
 |
| Jolie décoration pour ce ballon de foot : les centres des étoiles sont aux sommets d'un icosaèdre régulier. | Icosaèdre à la "Léonard de Vinci" réalisé par Patrice Gaumeton, ébéniste à Paris. | Radiolaire icosaédrique dessiné par Ernst Haeckel en 1887. |

Logo d'un centre de recherche reprenant la construction de l'icosaèdre. |
 |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014