Hypericosaèdre

HYPERICOSAÈDRE
600-cell, 600-Zell

Famille	polychores réguliers
Historique	découvert par Ludwig Schläfli en 1851
Autres noms	C₆₀₀, 600 cellules, hexacosichore (de hexacosi venant du grec exakósia "600" et chore "cellule"), tétraplexe (abréviation de "complexe de tétraèdres") ou polytétraèdre.
Dual	hyperdodécaèdre
Symbole de Schläfli	{3, 3, 5} (5 tétraèdres réguliers autour de chaque arête)
Cellules	600 tétraèdres réguliers
Sommets	120 sommets ; à chaque sommet aboutissent 12 arêtes, 30 faces et 20 cellules
Base de calotte	icosaèdre
Arêtes	720 arêtes de longueur a ; chaque arête est commune à 5 faces et à 5 cellules
Faces	1200 triangles
Patron	environ 8.10³⁰⁸ patrons différents en tout
Graphe des arêtes	non représenté : il a 120 sommets de degré 12 ! Voir ici des renseignements suppplémentaires
Diamètres	hypersphère inscrite : ...a ; hypersphère circonscrite : ????
Mensurations	hypervolume : volume de la frontière :
Coordonnées des sommets	(±1, ±1, ±1, ±1) et ses permutés : 16 sommets (0, 0, 0, ±2) et ses permutés : 8 sommets (±1, ±phi, ±1/phi, 0) et ses permutés pairs : 96 sommets où phi est le nombre d'or (1+sqrt(5))/2 pour une longueur d'arête a = 2/phi.
Construction	Voir [Lo Jacomo] page 80
Plans de symétrie	15
Groupe des isométries	d'ordre 120²= 14400
Sites	en.wikipedia.org/wiki/600-cell mathworld.wolfram.com/600-Cell.html www.polytope.de/c600.html www.bathsheba.com/math/600cell/index.html images.math.cnrs.fr/imagedumoment/le-120-cell/

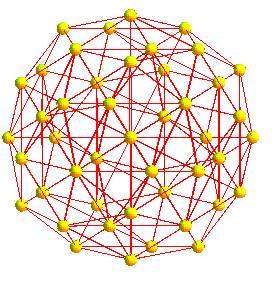
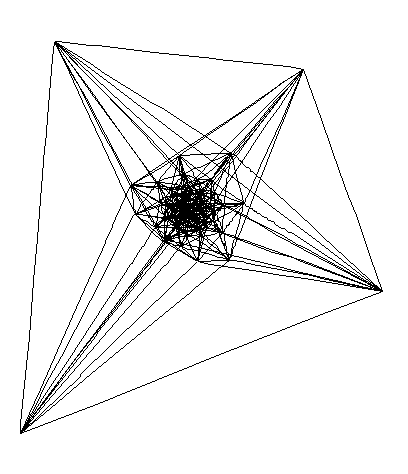
Gravures représentant l'hypericosaèdre réalisées par Patrice Jeener, avec son aimable autorisation.