Hexacontaèdre trapézoïdal

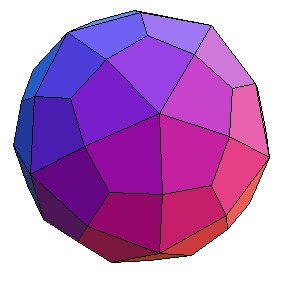
HEXACONTAÈDRE TRAPÉZOÏDAL
Trapezoidal hexecontahedron, Deltoidhexakontaeder

Famille

polyèdre semi-régulier de deuxième espèce, polyèdre de Catalan

Historique

étudié par Catalan en 1862

Etymologie

hexaconta = 60 ; les faces ne sont pas des trapèzes, mais des cerfs-volants ; il ne doit pas y avoir de terme grec ancien pour les cerfs-volants (chartaetós en grec moderne).

Autres noms

hexacontaèdre deltoïdal, hexacontaèdre tétragonal

Dual

rhombicosidodécaèdre

Faces

60 cerfs-volants formés de deux triangles isocèles d'angles au sommet

Sommets

62, dont 20 sommets de degré 3, de code de Schläfli 4³, 30 sommets de degré 4 de code 4⁴et 12 sommets de degré 5 de code 4⁵
^{Les coordonnées des sommets sont données
ci-dessous.}

Arêtes

120, dont 60 arêtes de longueur a et 60 arêtes de longueur

.
angle dièdre :

Patron et graphe

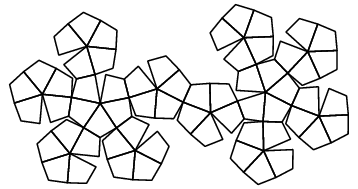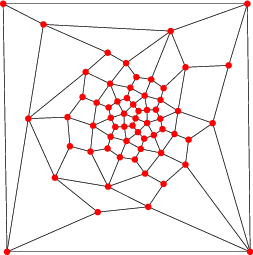Diamètres

sphère inscrite : 3,42 ; sphère circonscrite

Mensurations

volume : 22,21 a³ aire : 38,92 a².
coefficient isopérimétrique : 0,95.

Construction

icosidodécaèdre: augmenté sur chaque face d'une pyramide droite (20 pyramides triangulaires et 12 pentagonales)
La somme d'un icosidodécaèdre (en jaune ci-contre) et de son dual le triacontaèdre rhombique (en rouge ci-contre) donne un "polyèdre" (dont les faces sont des cerfs-volants gauches) équivalent à l'hexacontaèdre trapézoïdal (il est inscrit dans une sphère, et non circonscrit).

Groupe des isométries

= celui du dodécaèdre

Si l'on partage les 20 faces d'un icosaèdre en trois à partir du centre, ou les 12 faces d'un dodécaèdre en six à partir du centre, on obtient deux "polyèdres" (dont certaines faces sont coplanaires) ayant la structure de l'hexacontaèdre trapézoïdal.

On peut passer continûment de l'un à l'autre ; on obtient l'hexacontaèdre semi-régulier lorsque les angles dièdres entre les faces sont égaux.

Les hexacontaèdres intermédiaires ci-dessus ont pour sommets, en fonction du nombre d'or

:
- les douze

et permutés (formant un icosaèdre), comme le point A ci-contre
- les six

et permutés circulaires et les vingt-quatre

et permutés circulaires (formant un icosidodécaèdre), comme le point B ci-contre
- les huit

et les douze

et permutés circulaires (formant un dodécaèdre), comme le point C ci-contre.

Le paramètre k variant de k = 1/2 (cas de l'icosaèdre) à (cas du dodécaèdre).

Le cas semi-régulier est obtenu pour , avec une longueur de grande arête .
Les points A et B sont cosphériques pour (figure centrale).
Pour k = 2, on obtient un hexacontaèdre non convexe, à faces losanges, appelé "hexacontaèdre rhombique" (à droite).

Voir la page d'Alain Esculier expliquant le principe de cette expansion.

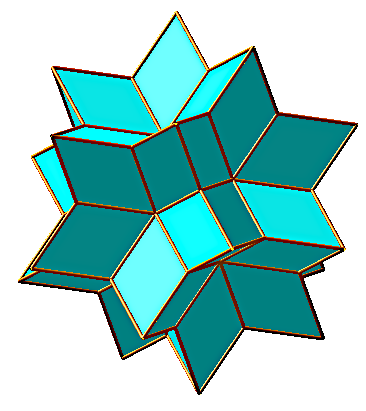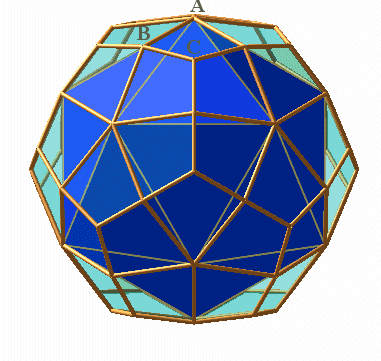
L'intersection de 6 prismes décagonaux réguliers pleins dont les axes sont les diagonales d'un icosaèdre (ou les diagonales faciales d'un dodécaèdre) forme un solide dont la surface est un polyèdre équivalent à l'hexacontaèdre, obtenu pour

dans la définition précédente.
Remarquer que chacune des 10 faces d'un prisme fournit 10 faces du polyèdre, qui possède donc bien 60 faces.

Les faces sont des cerfs-volants d'angles :

L'intersection de 6 cylindres de révolution pleins dont les axes sont les diagonales d'un icosaèdre (ou les diagonales faciales d'un dodécaèdre) forme un solide de Steinmetz dont la surface a une structure d'hexacontaèdre trapézoïdal (chaque cylindre forme un ruban composé de 10 "faces" du (faux) polyèdre) .