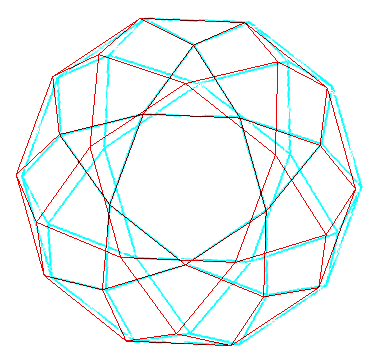
Anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite)
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
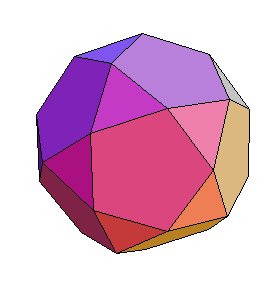
ICOSIDODÉCAÈDRE
Icosidodecahedron, Ikosidodekaeder
.
Anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite) |
 |
| Etymologie : De "icosi " 20, et "dodéca"
12 car il a 20 faces triangulaires et 12 faces pentagonales ; c'est aussi
l'intersection d'un icosaèdre et d'un dodécaèdre
; le nom a été donné par Képler.
Vues Povray de cette page réalisées par Alain Esculier. |
| Famille | polyèdre semi-régulier ou polyèdre d'Archimède | ||||||
| Historique | solide connu d'Archimède (IIIe s. av. J.C.) | ||||||
| Dual | Triacontaèdre
rhombique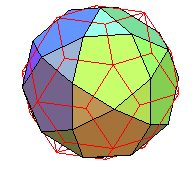 |
||||||
| Faces | 20 triangles et 12 pentagones | ||||||
| Sommets | 30 sommets de degré 4, de code de Schläfli 3.5.3.5 | ||||||
| Arêtes | 60 arêtes de longueur a ; angle dièdre
: |
||||||
| Patron et graphe |
 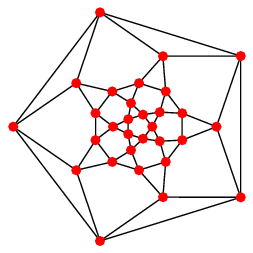 |
||||||
| Diamètres | sphère inscrite dans les pentagones : intersphère (passant par les milieux des arêtes) : |
||||||
| Coordonnées des 30 sommets | |||||||
| Équations des plans faces
d'où : équation cartésienne de la surface |
12 + 8 triangles : d'où l'équation 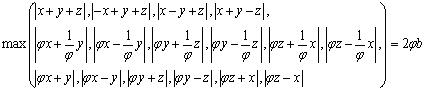 |
||||||
| Équations des 6 plans passant par O contenant
les arêtes,
d'où : équation cartésienne de la surface |
d'où l'équation |
||||||
| Mensurations | volume : coefficient isopérimétrique : |
||||||
| Constructions |
|
||||||
| Plans de symétrie | 15 | ||||||
| Axes de rotation |
|
||||||
| Groupe des isométries | = celui de l'icosaèdre | ||||||
| Polyèdres dérivés | par troncature forte
: polyèdre équivalent au rhombicosidodécaèdre
;
par troncature faible : polyèdre équivalent à l'icosidodécaèdre tronqué ; par augmentation : hexacontaèdre trapézoïdal voir aussi le dodécadodécaèdre, le grand dodécahémicosaèdre et le petit dodécahémicosaèdre qui ont les mêmes sommets, ainsi que grand icosidodécaèdre, le grand dodécahémidodécaèdre et le grand icosihémidodécaèdre. |
| Comme pour l'octaèdre,
et le cuboctaèdre,
les arêtes de l'icosidodécaèdre se regroupent en un
certain nombre de polygones réguliers ; ici, en six décagones.
Par projection centrale sur la sphère circonscrite, on obtient six grands cercles (voir les équations des six plans de ces six cercles à surface de Goursat). |
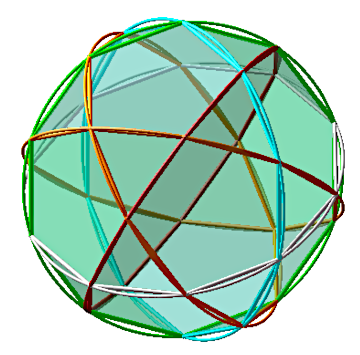 |
 |
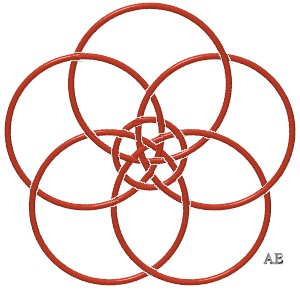
| On peut entrelacer dessus-dessous ces cercles de sorte
à obtenir un entrelac
premier à six composantes non nouées et trente croisements.
A droite, projection stéréographique de ces six cercles, donnant la représentation "plane" de l'entrelac. On vérifiera que les composantes sont deux à deux enlacées. |
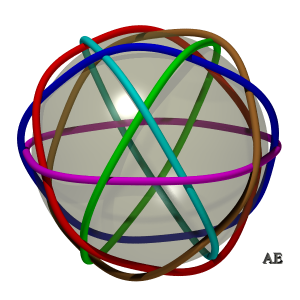 |
 |
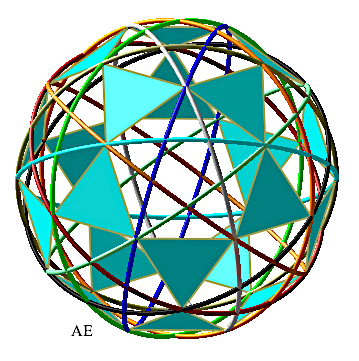
| Une propriété remarquable de l'icosidodécaèdre
est que les distances angulaires en degré entre deux des 60 sommets
(imégés comme des villes) sont toutes rationnelles et que
60 est le maximum possible pour cette propriété (sauf le
cas où les "villes" seraient "alignées" sur un grand cercle).
Par exemple la distance entre deux "villes" voisines situé
sur un des grands cercle précédents est de 360/10° =
36°.
|
 |
|
| Ballon à tressage icosidodécaèdrique
servant dans un jeu traditionnel aux Philippines.
Et tressage icosidodécaèdrique plus moderne.
|
 |
 |
 |
Les coutures du ballon jaune ci-contre suivent une structure icosidodécaédrique, et non celle d'un icosaèdre tronqué comme d'habitude. Pour le ballon de droite, ce sont les décorations qui sont, elles, icosidodécaédriques et reprennent l'entrelacs vu ci-dessus. |
| Si on pose l'icosidodécaèdre sur une face pentagonale et si on fait pivoter la moitié supérieure d'un dixième de tour, on obtient un polyèdre qui n'est plus semi-régulier mais reste inscriptible à faces régulières, dénommé pseudo-icosidodécaèdre ou, suivant la terminologie de Johnson orthobirotonde pentagonale (J 34). | 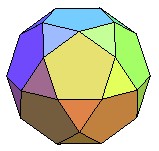 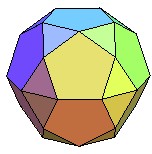 |
 . . |
 |
|
Objet icosidodécaédrique photographié au musée du compagnonage à Tours |
Polyèdre composé de l'icosaèdre et de son dodécaèdre dual polaire par rapport à l'intersphère ; l'intersection donne l'icosidodécaèdre. |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2022