Dodécaèdre

DODÉCAÈDRE
Dodecahedron, Dodekaeder

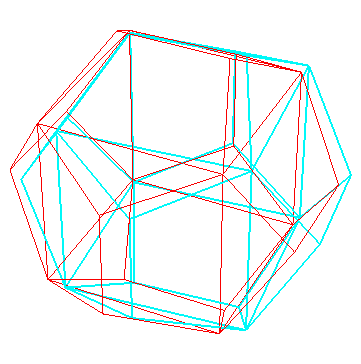
Anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite)

Du grec "Dodeka" douze et "edros" siège, base.
Vues Povray de cette page réalisées par Alain Esculier.
Lien : mathematische-basteleien.de/pentagondodekaeder.htm

Un dodécaèdre est un polyèdre à 12 faces.

Il existe plus de 6 millions de types de dodécaèdres différents dont voici la répartition suivant le nombre de sommets :

Nombre de sommets 8 9 10 11 12 13 14 15 16 17 18 19 20

Nombre de dodécaèdres 14 558 8822 64439 268394 709302 1263032 1556952 1338853 789749 306470 70454 7595

Le plus célèbre est le dodécaèdre régulier, ou dodécaèdre pentagonal (20 sommets), dont on trouvera ci-dessous la carte de visite ; mais il y a aussi le dodécaèdre rhombique (14 sommets), le triaki-tétraèdre (8 sommets) et le dodécadeltaèdre (8 sommets). Voir ici une liste plus complète.

Famille polyèdres réguliers

Historique 10 siècles av. JC, les Étrusques utilisaient des dés dodécaèdriques ; solide décrit par Platon en 370 av. J.C.

Dual icosaèdre régulier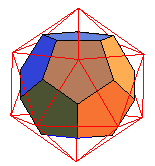 ¬ dual polaire du dodécaèdre par rapport à sa sphère circonscrite

Faces 12 pentagones réguliers

Sommets 20 sommets de degré 3, de code de Schläfli 5³

Arêtes 30 arêtes de longueur a ; angle dièdre : rd, soit 116° 33' 54"

Patrons  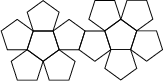  (il y en a 43 380 en tout !)

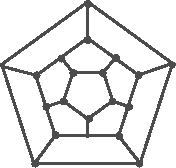Graphe       Comparer avec une citadelle de Vauban !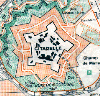 Ce graphe n'est pas semi-eulérien (il n'y a pas de chemin passant une fois exactement par chaque arête) mais il est hamiltonien : il existe un chemin fermé passant une fois exactement par chaque sommet ; voir la réponse plus bas.

Chaque face étant entourée d'un nombre impair de faces contiguës, ses faces sont coloriables avec au moins 4 couleurs (et aussi au plus !).

Diamètres sphère inscrite : ; intersphère (tangente aux arêtes) : ;
sphère circonscrite : où est le nombre d'or.

Mensurations volume : 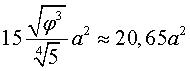    aire :   rapport volume/(volume de la sphère circonscrite) : 66%
coefficient isopérimétrique :

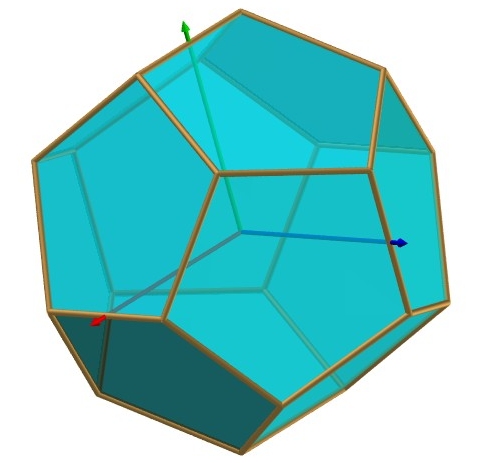
Coordonnées
des sommets
(voir le repère dans
la vue principale ci-dessus) 12 sommets permutés circulairement, et 8 sommets d'un cube où ,
2 sommets étant reliés par une arête ssi leur distance vaut a.

Équations des 6 plans des faces

Équation de la surface (idée Bernard Dupuy)

Constructions

n°1 : comme dual de l'icosaèdre.

n°2 : cube augmenté de 6 "toits"
les faîtes sont les grands côtés de 3 rectangles perpendiculaires entre eux
dont les côtés sont proportionnels au nombre d’or et à l’inverse du nombre d’or.
Voir aussi l'anaglyphe en haut de page.

Le toit de faîte [KH] surmontant le carré ABCD
est entièrement défini par le fait que ses arêtes
([AH], [KH], etc) ont même longueur et forment
entre elles des angles égaux (AHB = AHK etc).

n° 3 : comme cube tronqué aux arêtes (construction équivalente à la précédente) : voir une animation ci-dessous.

n° 4 : comme antidiamant tronqué.

Plans de symétrie 15

Axes de rotation

6 axes passant par 2 centres de faces opposées (4 rotations d'ordre 5 par axe)

15 axes passant par les milieux de 2 arêtes opposées (1 rotation d'ordre 2 par axe)

10 axes passant par 2 sommets opposés (2 rotations d'ordre 3 par axe)

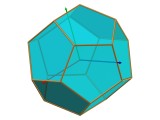Groupe des isométries ordre 120 : 60 rotations (l'identité, 12 cinquièmes de tours, 12 deux cinquièmes de tours, 20 tiers de tours, 15 demi-tours) et 60 antirotations (produits des précédentes par la symétrie de centre O, dont 15 réflexions)
Le sous-groupe des 60 rotations est isomorphe au groupe A₅ des permutations paires de 5 objets (action sur un ensemble de 5 tétraèdres réguliers inscrits).

Polyèdres dérivés par troncature forte : icosidodécaèdre ;
par troncature faible : dodécaèdre tronqué ;
par facettage : icosidodécaèdre tronqué ;
par augmentation : pentaki-dodécaèdre, triacontaèdre rhombique.
le grand dodécaèdre étoilé à les mêmes sommets que le dodécaèdre.
voir aussi l'hyperdodécaèdre et les surfaces de Goursat.

Animation de la construction du dodécaèdre par troncature des douze arêtes du cube (fournissant les douze faces du dodécaèdre). Une construction approchée très simple :
prendre un cube (qui fournit 8 sommets du dodécaèdre) et le faire tourner de 45° autour d'une diagonale (cela fournit 6 autres sommets) et compléter les 6 sommets restants par symétrie.
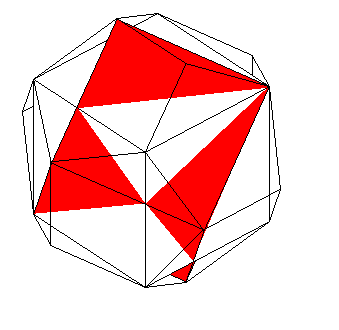
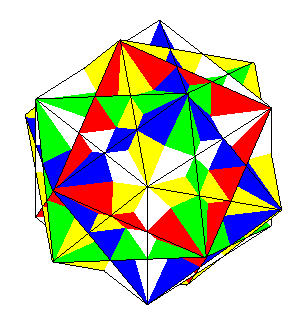
En fait l'angle de rotation exact est valant environ 44,5°. Si on effectue ces rotations pour chaque diagonale du cube, on on obtient un composé de 5 cubes dont les sommets sont ceux du dodécaèdre régulier et les arêtes celles du petit icosidodécaèdre ditrigonal et deux de ses cousins.

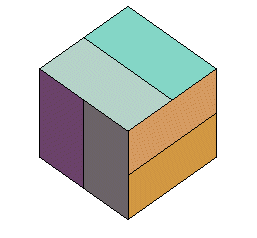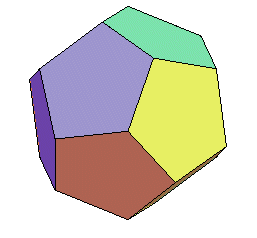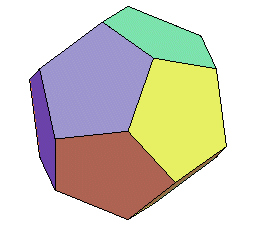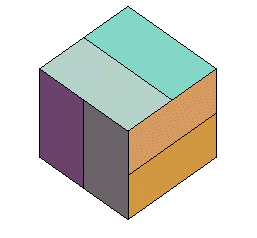
L'animation ci-contre fait passer du cube au dodécaèdre rhombique en passant par le dodécaèdre régulier; les sommets du cube restent fixes, et six "toits" sont posés sur les faces du cube. Les extrémités des six faîtes décrivent des segments de droite.
Les coordonnées des sommets du cube : (±1, ±1, ±1).
Les coordonnées des 12 autres sommets sont les permutations de : (0, ±(1+ h), ±(1– h²)), où h est la "hauteur" du toit.
Pour h = (rac(5)–1)/2 (inverse du nombre d'or), on obtient le dodécaèdre régulier.
Les polyèdres obtenus ont été dénommés pyritoèdres, voir des explications sur ce site.

Voici un cycle hamiltonien du graphe du dodécaèdre ; on peut montrer que c'est le seul, à isométrie du dodécaèdre près.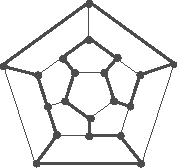

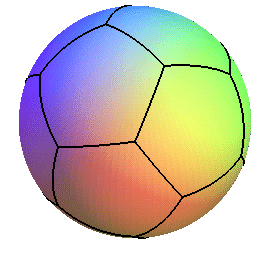Projection centrale du squelette du dodécaèdre sur la sphère circonscrite : on obtient un pavage régulier de la sphère par 12 pentagones sphériques réguliers ; remarquons qu'il est impossible de paver le plan avec des pentagones réguliers !

Le dodécaedre étant le polyèdre régulier ayant le maximum de sommets, le nombre maximal de calottes sphériques que l'on peut placer sur la sphère de sorte que chacune soit tangente à un même nombre d'autres calottes est égal à 20, et leurs centres sont au sommet d'un dodécaèdre régulier.
Cependant, cette configuration ne donne pas la réponse au problème des dictateurs ennemis dans le cas n = 20, problème demandant comment sont disposées sur une sphère n calottes sphériques identiques (les états de chaque dicateur) de taille maximale et ne se chevauchant pas. On sent bien qu'il y a encore beaucoup de bleu par rapport au rouge...
On ne connait pas actuellement la configuration optimale.
Sources : Marcel Berger, Pour la Science 176, p. 72 et dossier Pour la Science 41 p. 40.

Polyèdre composé formé du dodécaèdre et de l'icosaèdre dual polaire par rapport à la sphère tangente aux arêtes ; la partie commune est l'icosidodécaèdre. L'enveloppe des sommets est le triacontaèdre rhombique.

Dodécaèdre avec pavage d'Escher
Un plancton dodécaédrique !

Foot et dodécaèdre...

Superbe casse-tête dodécaédrique
Vu au Trait en Seine Maritime
Dodécaèdre gallo-romain en bronze (musée de Besançon)

La Cène vue par Dali
Dodécaèdre en tickets de métro.

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

Nombre de sommets	8	9	10	11	12	13	14	15	16	17	18	19	20
Nombre de dodécaèdres	14	558	8822	64439	268394	709302	1263032	1556952	1338853	789749	306470	70454	7595

Animation de la construction du dodécaèdre par troncature des douze arêtes du cube (fournissant les douze faces du dodécaèdre).	Une construction approchée très simple : prendre un cube (qui fournit 8 sommets du dodécaèdre) et le faire tourner de 45° autour d'une diagonale (cela fournit 6 autres sommets) et compléter les 6 sommets restants par symétrie. En fait l'angle de rotation exact est valant environ 44,5°.	Si on effectue ces rotations pour chaque diagonale du cube, on on obtient un composé de 5 cubes dont les sommets sont ceux du dodécaèdre régulier et les arêtes celles du petit icosidodécaèdre ditrigonal et deux de ses cousins.

Dodécaèdre avec pavage d'Escher	Un plancton dodécaédrique !	Foot et dodécaèdre...
Superbe casse-tête dodécaédrique	Vu au Trait en Seine Maritime	Dodécaèdre gallo-romain en bronze (musée de Besançon)