et ils résultent aussi de l'augmentation
d'un antiprisme par deux pyramides
(fig 2).
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ANTIDIAMANT
Antidiamond , Antidiamant
| Autres noms : trapézoèdre, deltoèdre. |
Un antidiamant d'ordre n est un polyèdre
ayant 2 sommets de degré n, chacune des faces aboutissant
à l'un des sommets étant contiguë exactement à
deux faces aboutissant à l'autre.
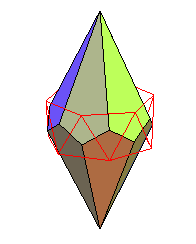
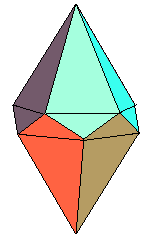
| Les antidiamant sont les duaux
des antiprismes (fig 1),
et ils résultent aussi de l'augmentation
d'un antiprisme par deux pyramides
(fig 2).
|
fig 1  |
 |
L'antidiamant est dit droit s'il est à symétrie
de rotation d'ordre n autour de l'axe des sommets de degré
n.
| Le seul antidiamant qui soit à faces régulières
est le cube, et il est antidiamant de 3 façons différentes.
D'autre part il y a, pour un ordre donné et à similitude près un seul antidiamant à sommets latéraux réguliers. C'est alors un polyèdre semi-régulier de deuxième espèce. |
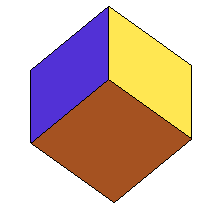 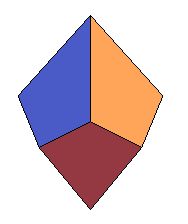 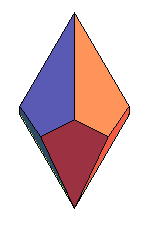
Antidiamants semi-réguliers d'ordre 3, 4 et 5. |
| Les antidiamants d'ordre 3 sont les rhomboèdres.
A part ce cas, l'antidiamant droit ne peut avoir ses arêtes égales. |
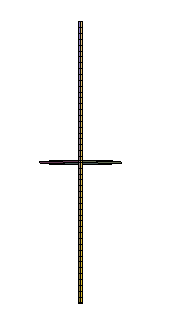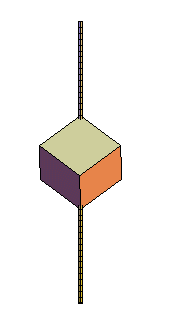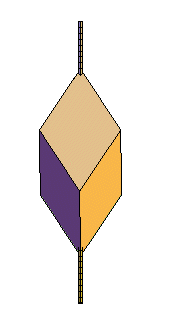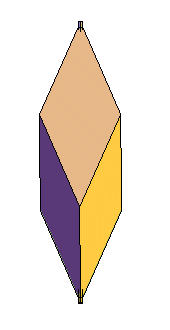 |
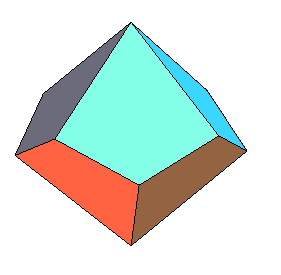
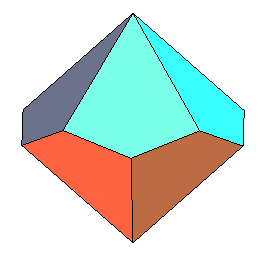
| Il n'existe, pour un ordre donné et à similitude
près, qu'un antidiamant droit inscriptible.
Pour n = 3, on retrouve évidemment le cube, mais voici ci-contre les cas n = 4 et 5. |
  |
Carte de visite de l'antidiamant droit d'ordre n :
| Faces | 2n cerfs-volants. |
| Sommets | 2 sommets de degré n, n de degré 3. |
| Arêtes | 3n arêtes, 2n d'un type, n d'un autre. |
| Coordonnées
des sommets |
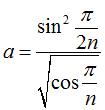 pour l'antidiamant droit inscriptible.
pour l'antidiamant droit inscriptible. |
| Faces correspondantes |
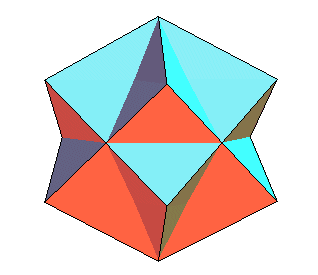
| Une généralisation : antidiamant à faces croisées : |
 |
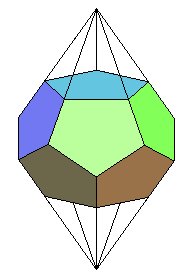
| Polyèdre dérivé : l'antidiamant
tronqué, plus familièrement appelé tambour,
obtenu par troncature des sommets d'ordre n. Il possède donc
2n faces latérales pentagonales et 2 faces n-gonales.
L'un des tambours réguliers pentagonaux n'est autre que le dodécaèdre régulier, représenté ci-contre. |
 |
| Dé en forme d'antidiamant d'ordre 5 (à 10 faces numérotées de 0 à 9) : |
 |
| La célèbre gravure d'Escher intitulée "étoiles" représente entre autres un antidiamant, à retrouver (quel ordre ?). |  |
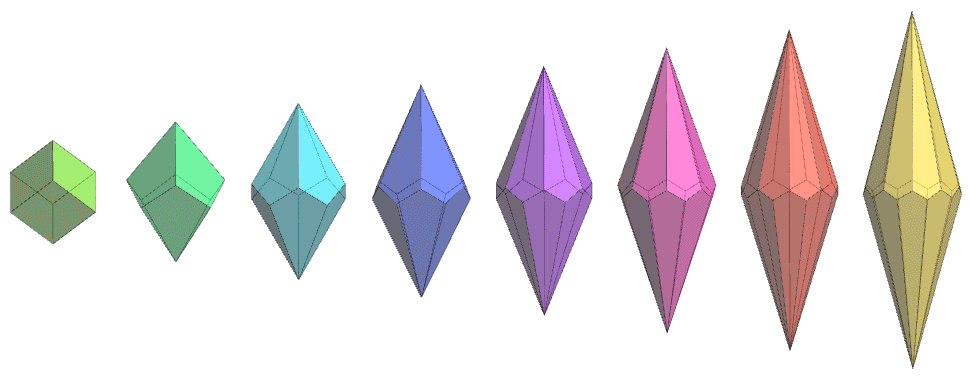
Série d'antidiamants semi-réguliers, par René
Ebel.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014