Pyramide

PYRAMIDE

Du latin pyramis "pyramide", provenant lui même du grec.
Lien : mathematische-basteleien.de/pyramid.htm

Une pyramide est un polyèdre ayant une face (sa base) dont les sommets sont joints par des arêtes à un même sommet (son sommet), formant les autres faces, dites faces latérales. L'ordre de la pyramide est celui de sa base.

Les pyramides sont aux polyèdres ce que les cônes sont aux surfaces (tandis que les prismes sont aux polyèdres ce que les cylindres sont aux surfaces).

Le volume d'une pyramide est le tiers du produit de l'aire de sa base par la distance du sommet au plan de la base.

Le dual d'une pyramide convexe est une pyramide du même type.

Un tétraèdre est de 4 façons différentes une pyramide.

La seule pyramide qui soit un polyèdre régulier est le tétraèdre régulier, et il n'y a que trois pyramides à faces régulières (autrement dit équilatérales), d'ordre 3, 4 ou 5 (les deux dernières étant des solides de Johnson, n° 1 et 2, et des polyèdres IFR). Une pyramide est à faces régulières ssi toutes les arêtes sont de même longueur.
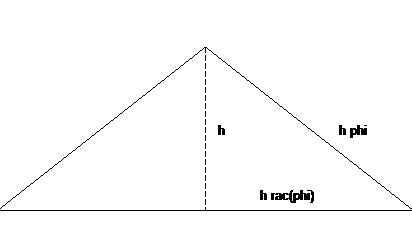
La hauteur de la pyramide à faces régulières à n côtés de longueurs a est , d'où .

On désigne cependant couramment par pyramide régulière une pyramide dont les faces latérales sont des triangles isocèles isométriques ; la base est alors un polygone régulier, et le sommet se projette sur la base en son centre.

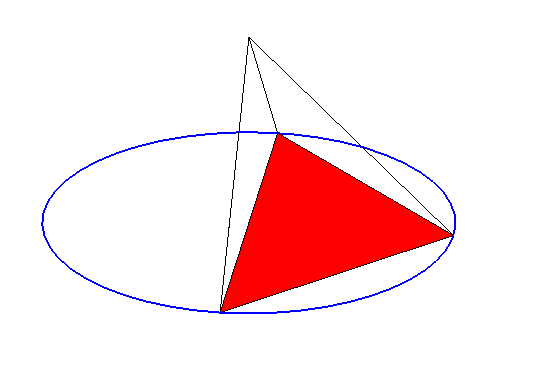
Attention 1 : une pyramide peut avoir ses faces latérales isocèles sans être régulière (voir ci-contre)
Attention 2 : une pyramide peut avoir toutes ses faces latérales isométriques sans être régulière, comme par exemple le tétraèdre équifacial.

On peut étendre la notion de pyramide au cas de bases qui sont des polygones croisés.
Ci- contre, une pyramide de base un pentagone croisé.

Voir aussi les bipyramides et les hyperpyramides.

D'après Hérodote (mais ce serait une légende), les pyramides de Chéops ont été construites de sorte que l'aire de chaque face latérale soit égale au carré de la hauteur.
Un petit calcul montre alors que la hauteur h et le côté a de la base sont reliés par la relation où est le nombre d'or. Le triangle rectangle joignant le sommet, le centre de la base et le milieu d'un côté est alors un triangle de Képler, de côtés de longueur , de sorte que la vision de face d'une pyramide donne un triangle formé de deux triangles de Képler accolés.
Et si l est la longueur de l'arête 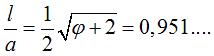; les faces sont donc presque équilatérales.
De plus est proche de ... Vue de face d'une pyramide.

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

La seule pyramide qui soit un polyèdre régulier est le tétraèdre régulier, et il n'y a que trois pyramides à faces régulières (autrement dit équilatérales), d'ordre 3, 4 ou 5 (les deux dernières étant des solides de Johnson, n° 1 et 2, et des polyèdres IFR). Une pyramide est à faces régulières ssi toutes les arêtes sont de même longueur. La hauteur de la pyramide à faces régulières à n côtés de longueurs a est , d'où .
On désigne cependant couramment par pyramide régulière une pyramide dont les faces latérales sont des triangles isocèles isométriques ; la base est alors un polygone régulier, et le sommet se projette sur la base en son centre.
Attention 1 : une pyramide peut avoir ses faces latérales isocèles sans être régulière (voir ci-contre) Attention 2 : une pyramide peut avoir toutes ses faces latérales isométriques sans être régulière, comme par exemple le tétraèdre équifacial.