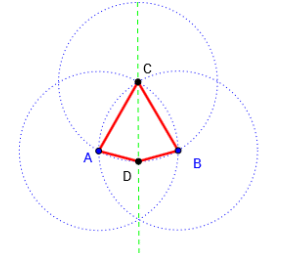
C'est un triangle équilatéral dont un côté a été modifié comme montré ci-contre.
Son périmètre vaut
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
QUADRILATÈRE
Quadrilateral, Viereck
Un quadrilatère est un polygone à 4 côtés.
Remarque : par régularité avec les ordres supérieurs, un quadrilatère devrait s'appeler un tétragone. Mais tétragone ne désigne, au féminin, qu'une espèce d'épinard, ainsi désignée à cause de la forme de ses graines.
Les quadrilatères dont deux côtés sont parallèles sont les trapèzes.
Les quadrilatères à diagonales perpendiculaires sont dits orthodiagonaux, avec comme cas particuliers les cerf-volants.
Les quadrilatères à côtés opposés parallèles, ou à diagonales se coupant en leur milieu sont les parallélogrammes.
Les quadrilatères équilatéraux (à côtés de même longueur) sont les losanges : ce sont les parallélogrammes orthodiagonaux.
Les quadrilatères à angles droits sont les rectangles.
Les quadrilatères réguliers
sont les carrés ; ce sont les
losanges rectangles.
| Le quadrilatère de diamètre unité
ayant la plus grande aire est le carré. Mais ce n'est plus vrai
pour le quadrilatère de plus grand périmètre : c'est
le cerf-volant de Tamvakis, découvert en 1987.
C'est un triangle équilatéral dont un côté a été modifié comme montré ci-contre. Son périmètre vaut |
 |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2022