Du grec polus "plusieurs", gonia, "angle".

Un polygone est un ensemble fini non vide de segments de droites (non réduits à un point), inclus dans un même plan, tels que
    1) chaque extrémité de chaque segment coïncide avec une extrémité d'un seul autre segment de l'ensemble, non aligné avec le premier.
    2) deux extrémités de segments sont toujours reliés par une suite de segments ayant chacun une extrémité en commun avec le suivant (condition de connexité).
    3) deux segments n'ont aucun point intérieur en commun (condition de non croisement - sans la condition 3, on a la notion de polygone croisé, ou complexe).

Ces segments sont les côtés du polygone, leurs extrémités en sont les sommets, les droites qui les portent, les côtés prolongés.

Un polygone possède au moins 3 sommets et 3 côtés.

On classe les polygones suivant leur nombre de côtés, appelé l'ordre du polygone, en utilisant les suffixes grecs suivants :
 

		3	4	5	6	7	8	9	10
		cas à part triangle	cas à part quadrilatère	penta	hexa	hepta	octo	ennéa	déca

 

11	12	13	14	15	16	17	18	19	20
hendéca ou undéca	dodéca	tridéca	tétradéca	le suffixe ...	...ci-dessus..	plus déca	...	...	icosa

 

21	22	23	24	25	26	27	28	29	30
icosiéna	icosidi	icositri	icositétra	icosi plus le...	...suffixe....	...ci-dessus	...	...	triaconta

 

31	33		40	50	60	70	80	90	100	1000	10000
triacontaéna	triacontadi	etc.	tétraconta	pentaconta	hexaconta	heptaconta	octaconta	ennéaconta	hecta	chilia	myria

La ligne polygonale associée est la réunion des côtés ; pour un polygone non croisé, c'est une courbe de Jordan, séparant le plan en deux parties, l'une formée des points dits "intérieurs" au polygone, l'autre formée des points dits "extérieurs".
Le polygone plein est la réunion de l'ensemble des points intérieurs et de la ligne polygonale.

La ligne polygonale étant orientée dans le sens trigonométrique, l'angle du polygone en un sommet B, les sommets précédents et suivants étant A et C est la mesure de l'angle  ; la somme des angles d'un polygone d'ordre n est . Un polygone dont les angles sont droits est appelé un orthogone.

Le polygone est dit convexe si le polygone plein est convexe ; ce polygone plein est alors l'enveloppe convexe des sommets ; et une partie bornée du plan est un polygone plein convexe sssi c'est une intersection d'un nombre fini de demi-plans fermés.
On peut aussi caractériser les polygones convexes par le fait que leurs angles sont saillants ().

Etant donné n réels >0, il existe un polygone convexe dont les côtés ont pour longueurs ces n nombres ssi chacun d'entre eux est strictement inférieur à la somme des autres (et l'ordre des côtés peut être choisi arbitrairement).
 

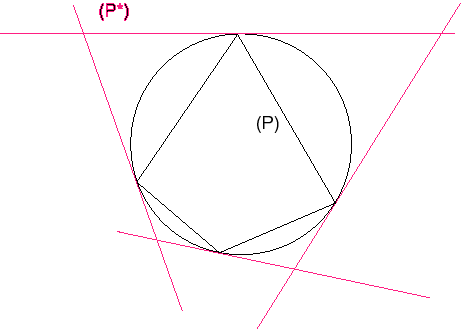
Un polygone est dit inscriptible si ses sommets sont sur un cercle ; il est alors convexe (si non croisé). Un polygone convexe est dit circonscriptible, si ses côtés prolongées sont tangents à un même cercle ; cette condition équivaut à ce que son dual obtenu par polarité par rapport à un cercle soit inscrit dans ce cercle. On démontre que parmi tous les polygones convexes dont les côtés ont des longueurs données dans un certain ordre, celui qui a la plus grande aire est celui qui est inscriptible.

 

Il est à noter que si, pour un polygone non croisé, la ligne polygonale est caractéristique du polygone, ce n'est plus vrai pour les polygones croisés, comme le montre le contre-exemple ci-contre, où la même ligne polygonale provient du polygone de côtés AB, BC, CD, EF, FA et aussi du polygone de côtés AB, BC, CF, FE, ED, DA.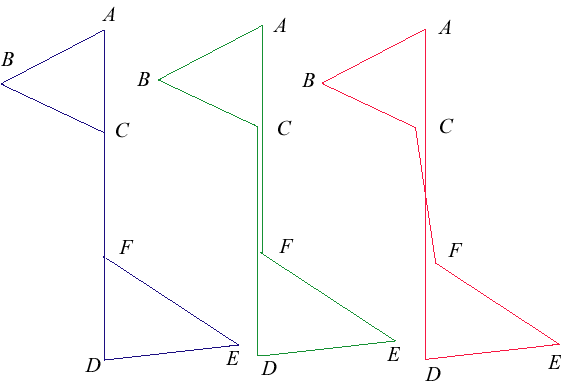

Voir aussi les polygones réguliers.
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2009