Un hexagone est un polygone à 6 côtés (et donc 6 sommets).

Il existe, à homothéties près, un seul hexagone régulier, qui est convexe. Voir les relations métriques dans l'hexagone régulier sur la page des polygones réguliers.

Il n'existe pas d'hexagone régulier de dont toutes les cordonnées sont entières, mais il en existe dans :  (centre O, situé dans le plan x + y + z = 0, côté  = )

Comme le montre le fond de cette page, l'hexagone régulier et ses déformations affines (c'est-à-dire les hexagones à côtés opposés parallèles) sont des parallélogones, c'est-à-dire qu'ils pavent le plan par translations.
 
 

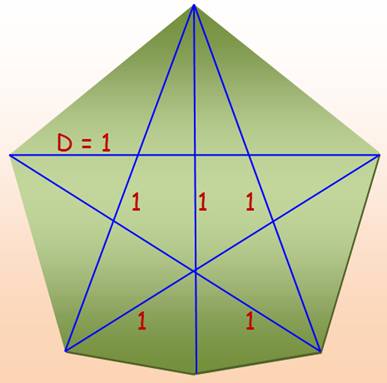
L'haxagone convexe de diamètre unité de plus grande aire n'est pas l'hexagone régulier, mais l'hexagone de Graham, découvert en 1974 (voir mathworld et l'article original). C'est un pentagone (non régulier) dont toutes les diagonales sont de longueur 1 et dont un côté a été modifié comme indiqué ci-contre.

Voir aussi l'hexagramme, et l'hexagone de Sierpinski.

Autre page : mathematische-basteleien.de/sechseck.htm
 

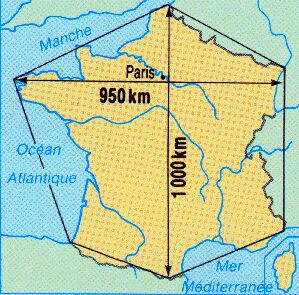
L'Hexagone !		Pavage hexagonal apicole
Damier du jeu de hex	Kalmia latifolia	Réseau de cercle formant des hexagones cuvilignes...

 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2016