Notion étudiée par Fedorov en 1885. Lien : www.iri.upc.edu/people/ros/StructuralTopology/ST2/st2-05-a1-ocr.pdf www.spektrum.de/lexikon/geowissenschaften/paralleloeder/11920

Un parallélogone est un polygone convexe qui, par translations, peut paver le plan (autrement dit le polygone plein et ses translatés ont deux à deux des intérieurs vides et une réunion égale au plan entier).

Fedorov a montré que les parallélogones sont constitués uniquement des polygones convexes à 4 ou 6 côtés ayant un centre de symétrie, autrement dit, les parallélogrammes et les hexazonogones (attention, le triangle pave aussi le plan, mais pas par translations uniquement).

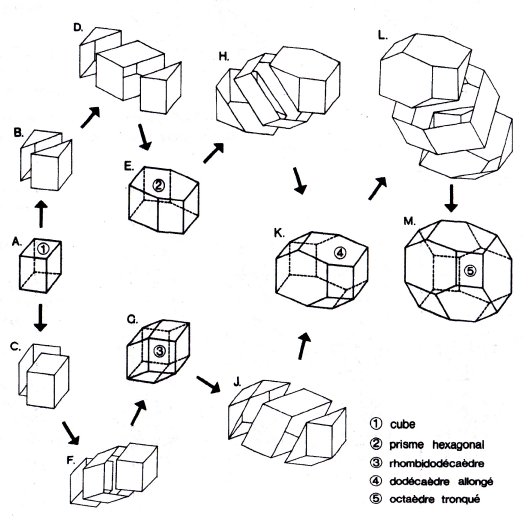
Un paralléloèdre est un polyèdre convexe qui, par translations, peut paver l'espace (autrement dit le polyèdre plein et ses translatés ont deux à deux des intersections d'intérieur vide et une réunion égale à l'espace entier).
 
 

Fedorov a montré que les paralléloèdres sont exactement les zonoèdres combinatoirement équivalents aux cinq polyèdres suivants :  le cube le prisme hexagonal le dodécaèdre rhombique le dodécaèdre rhombo-hexagonal ou dodécaèdre allongé l'octaèdre tronqué. La figure ci-contre, tirée de l'article ci-dessus intitulé habitat polyédrique, montre la construction des ces divers zonoèdres par élongation en partant du cube.

La notion équivalente en dimension n est celle de parallélotope généralisé.
 
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2015