PAVAGE MONOÉDRIQUE (ou pavage à mono-tuile)
Pavages dont tous les pavés sont isométriques.
On montre [Convex
polygons that cannot tile the plane. American Mathematical Monthly,
Vol. 85 (1978), 785-792] que, dans le cas convexe,
le polygone de base a six côtés au plus. Tous les triangles
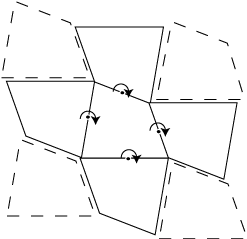
et quadrilatères convexes pavent le plan (ci-contre, une preuve
sans mots de ce dernier fait). Les hexagones convexes pavant le plan sont
ceux qui ont un centre de symétrie, autrement dit les 3-zonogones.
Pour les pentagones convexes, la
liste complète a été établie (sous-réserve
de vérification) en 2017 ; voir aussi cet
article de J.P. Delahaye.
Dans le cas non convexe, il a été trouvé
des pavages monoédriques non périodiques (voir à problème
einstein). |
|
PAVAGE ISOÉDRIQUE
Pavage "pavés-transitif", en ce sens que pour
tout couple de pavés, il existe une isométrie conservant
globalement le pavage, et envoyant un pavé sur l'autre ; il
est donc forcément monoédrique.
Ci-contre, un exemple
de pavage monoédrique qui n'est pas isoédrique.
Voir cet
article de J.P. Delahaye. |

Monoédrique NON isoédrique.
|
PAVAGE RÉGULIER
Un pavage polygonal est dit régulier s'il
est bord à bord et que tous ses pavés sont des polygones
réguliers de même type (on remarquera
que contrairement aux polyèdres, il n'est pas besoin de préciser
que les sommets sont de même degré).
A similitudes près, il en existe 3, appelés,
par analogie avec les polyèdres, "pavages de Platon", et répertoriés
sur la page des polyèdres réguliers.
Un drapeau étant une suite 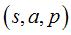 où p est un pavé du pavage polygonal à arêtes
jointives, a une arête de ce pavé, et s une
extrémité de cette arête, le pavage est régulier
ssi le groupe des isométries laissant le pavage invariant est transitif
sur les drapeaux, c'est-à-dire qu'il existe toujours une isométrie
envoyant un drapeau donné sur un drapeau donné.
où p est un pavé du pavage polygonal à arêtes
jointives, a une arête de ce pavé, et s une
extrémité de cette arête, le pavage est régulier
ssi le groupe des isométries laissant le pavage invariant est transitif
sur les drapeaux, c'est-à-dire qu'il existe toujours une isométrie
envoyant un drapeau donné sur un drapeau donné. |

|
| PAVAGE SEMI-RÉGULIER
Un pavage polygonal est dit semi-régulier
s'il est bord à bord, que tous ses pavés sont des polygones
réguliers, et que tous ses sommets sont identiques (en ce sens que
les pavés arrivant à ces sommets sont 2 à 2 du même
type, et dans le même ordre).
A similitudes près, et excepté les pavages
de Platon, il en existe 8, appelés par analogie avec les polyèdres,
"pavages d'Archimède", et répertoriés sur la page
des polyèdres d'Archimède.
Un pavage polygonal bord à bord est semi-régulier
ssi le groupe des isométries le laissant invariant est transitif
sur les sommets. |

|
| PAVAGE SEMI-RÉGULIER DE DEUXIÈME ESPÈCE
Pavage monoédrique bord à bord tel que tous
les angles des polygones arrivant à un sommet sont égaux.
Ce sont les duaux des pavages semi-réguliers.
A similitudes près, et excepté les pavages
de Platon, il en existe 8, appelés "pavages de Laves", et répertoriés
sur la page des polyèdres de
Catalan.
Un pavage est semi-régulier de deuxième
espèce ss'il est polygonal, bord à bord, et isoédrique.
|

|
PAVAGE KALÉIDOSCOPIQUE
Pavage monoédrique tel que les pavés voisins
d'un pavé donné sont obtenus par symétrie par rapport
à l'arête commune. Ce sont 6 des 8 pavages précédents
(enlever le pavage du Caire et celui à fleur). |

|
| PAVAGE POLYGONAL ÉTOILÉ
Cette notion est l'analogue plan des polyèdres
étoilés ; il ne s'agit plus de pavages formés
de parties compactes du plan, mais formés de polygones,
étoilés ou non, au sens d'ensembles d'arêtes, vérifiant
:
- deux polygones du pavage ont soit
exactement une arête en commun (ils sont jointifs), soit aucune
- (condition de connexité)
: étant donné deux polygones, il existe une succession de
polygones jointifs joignant l'un à l'autre
- étant donné un sommet
S
d'un des polygones du pavage, les segments [X,Y], où (X,S,Y)
est une succession de sommets de l'un des polygones du pavage, forment
l'ensemble des côtés d'un polygone (éventuellement
croisé) (nommé l'image-sommet de S)
- tout point du plan est dans l'enveloppe
convexe des sommets de l'un des polygones |
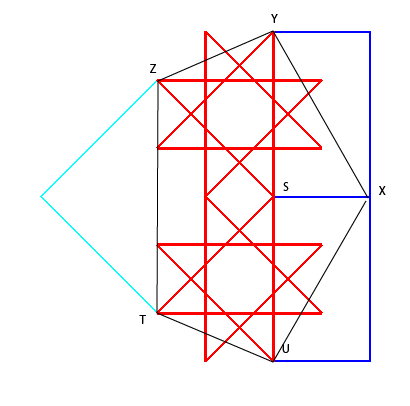 |
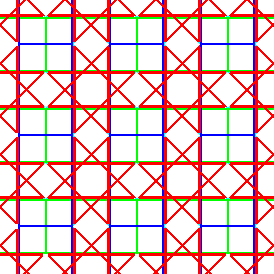
| Par exemple, dans le pavage ci-contre arrivent en chaque
sommet une étoile octogonale, un carré, une deuxième
étoile, et deux rectangles.
Au dessus, la figure-sommet d'un sommet S a été
indiquée en noir.
Il n'existe pas de pavage étoilé régulier
qui seraient les analogues de polyèdres de Képler-Poinsot,
mais 14 pavages étoilés semi-réguliers (voir
[Grunbaum Sheppard], p.632). |
|







