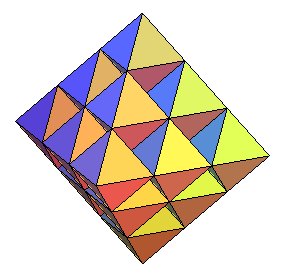
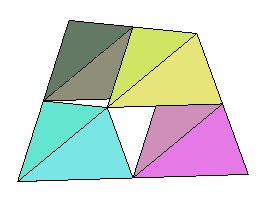
Le pavage octaédro-tétraédrique (tétraèdres manquants à gauche, octaèdre manquant à droite)
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
PAVAGE POLYÉDRIQUE
Polyhedral tiling or tessellation (or honeycomb), Raumfüllung
mit Polyedern
Un pavage polyédrique,
ou "nid d'abeilles" est un ensemble de polyèdres
pleins dont la réunion est égale à l'espace tout
entier et qui ne s'intersectent que sur leur frontière. Il est dit
bord
à bord (en anglais : face to face) si les polyèdres qui
ont une intersection non vide s'intersectent suivant exactement une face
: c'est alors l'équivalent non borné d'un polytope
4D.
On peut définir alors un pavage polyédrique
dual
en choisissant un sommet à l'intérieur de chaque pavé,
et en joignant par une arête deux sommets appartenant à deux
faces contiguës.
Lorsque les pavés sont inscriptibles, le sommet
du dual choisi est le centre de la sphère circonscrite, de sorte
que les arêtes du dual sont orthogonales aux faces du pavage de départ.
PAVAGES RÉGULIERS
Un pavage polyédrique est dit régulier
s'il est bord à bord et que tous ses pavés sont des polyèdres
réguliers de même type.
A similitudes près, il en existe un seul, celui
qui est constitué de cubes.
PAVAGES SEMI-RÉGULIERS
Un pavage polyédrique est dit semi-régulier
s'il est bord à bord, que tous ses pavés sont des polyèdres
réguliers, et que tous ses sommets sont identiques (en ce sens que
les pavés arrivant à ces sommets sont disposés exactement
de la même facon).
A similitudes près, et excepté le pavage
par des cubes, il n'en existe qu'un, celui formé par des octaèdres
et des tétraèdres
réguliers.
A chaque arête aboutit deux tétraèdres
et deux octaèdres.


PAVAGES UNIFORMES
Mêmes conditions que précédemment,
mais on accepte commes pavés tous les polyèdres semi-réguliers,
de première ou de deuxième espèce.
Voir ces
animations.
PAVAGES SEMI-RÉGULIERS DE DEUXIÈME ESPÈCE
Un pavage polyédrique est dit semi-régulier de deuxième espèce s'il est à bord à bord, que tous ses pavés sont isométriques entre eux, et que toutes les figures formées par les arêtes arrivant à un même sommet sont isométriques entre elles.
A similitudes près, et excepté le pavage cubique, il n'en existe qu'un, dual du précédent, le pavage par des dodécaèdres rhombiques.
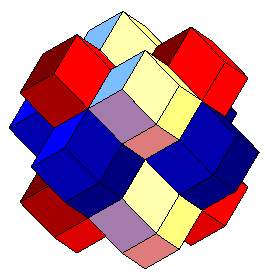
Voir aussi les paralléloèdres
(polyèdres pavant l'espace par translation), et les pavages
par des polytopes.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2015