OCTAÈDRE
Octahedron, Oktaeder

| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
OCTAÈDRE
Octahedron, Oktaeder

| Du grec "Okta" huit et "edros" siège,
base.
Autres noms : cocube (dual du cube), tétratétraèdre (intersection de deux tétraèdres). Lien : mathematische-basteleien.de/oktaeder.htm |
Un octaèdre est un polyèdre à huit faces.
Il existe 257 types
d'octaèdres dont voici la répartition suivant le nombre de
sommets :
| Nombre de sommets | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Nombre d'octaèdres | 2 | 11 | 42 | 74 | 76 | 38 | 14 |
On trouve par exemple le tétraèdre
tronqué, mais le plus célèbre octaèdre
est l'octaèdre régulier dont voici la carte de visite :
| autre nom | |||||||
| Famille | polyèdres réguliers, mais il fait aussi partie des antiprismes, ainsi que des diamants. | ||||||
| Dual | cube ,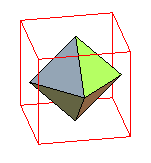 ¬
dual polaire de l'octaèdre par rapport à sa
sphère circonscrite
¬
dual polaire de l'octaèdre par rapport à sa
sphère circonscrite |
||||||
| faces | 8 triangles | ||||||
| Sommets | 6 sommets de degré 4, de code
de Schläfli 34
; angle solide
: |
||||||
| Arêtes | 12 arêtes de longueur a ; angle
dièdre : |
||||||
| Patrons |
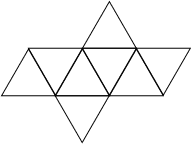 Il
y en a 11 en tout. Il
y en a 11 en tout. |
||||||
| Graphe des arêtes :
graphe octaédrique |
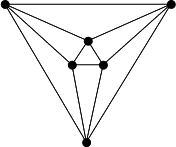 Voir
d'autres représentations sur mathworld. Voir
d'autres représentations sur mathworld. |
||||||
| Diamètres | sphère inscrite : |
||||||
| Mensurations | volume : a3 coefficient isopérimétrique : |
||||||
| Coordonnées
des sommets |
2 sommets étant reliés par une arête ss'ils n'ont pas des coordonnées opposées. Les sommets d'une face sont formés de 3 points où les coordonnées non nulles ne sont pas à la même place. |
||||||
| Équations des 8 plans faces
d'où : équation cartésienne de la surface |
|||||||
| Équations des 4 plans passant par O contenant
les arêtes,
d'où : équation cartésienne de la surface |
x = 0, y = 0, z = 0, d'où
l'équation : |
||||||
| Plans de symétrie | 3 contenant 4 arêtes, 6 passant par les milieux de 2 arêtes opposées et par 2 sommets. | ||||||
| Constructions | 1) tétraèdre.fortement
tronqué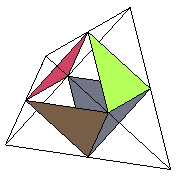
2) intersection de deux tétraèdres symétriques par rapport à leur centre 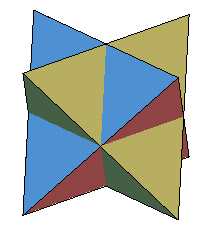
2) antiprisme à base triangulaire et faces régulières : 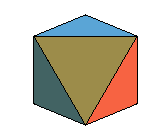 |
||||||
Axes de rotation
 |
|
||||||
| Groupe des isométries | ordre 48 : 24 rotations (l'identité, 6
quarts de tour, 8 tiers de tour, 9 demi-tours)
et 24 antirotations (produits des précédentes par la symétrie de centre O, dont 9 réflexions) Le sous-groupe des 24 rotations est isomorphe à S4. |
||||||
| Pavage | L'octaèdre régulier ne pave pas l'espace, mais il le fait en association avec le tétraèdre régulier, voir ci-dessous. | ||||||
| Polyèdres dérivés | par troncature forte
: cuboctaèdre ; par
troncature faible : octaèdre
tronqué ; par facettage : cuboctaèdre
tronqué ; par augmentation
: triaki-octaèdre,
dodécaèdre
rhombique ; hexaki-octaèdre
; par adoucissement : cube adouci.
Polyèdre croisé ayant les mêmes arêtes : le tétrahémihexaèdre. |
 |
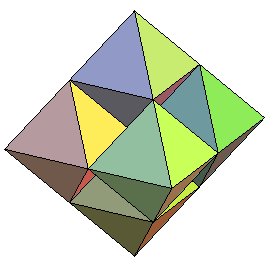
Construction d'un octaèdre à partir de
cubes, par la méthode de l'abbé René-Just Haüy
; on part d'un cube, on place 6 cubes sur chaque faces, puis 18 cubes de
façon à recouvrir toutes les faces, et ainsi de suite, en
ajoutant Voir l'article wikipedia sur les nombres octaédriques centrés. |
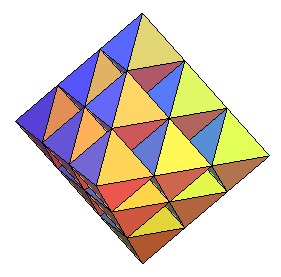
| Même disposition, mais avec des octaèdres.
La figure va finir par occuper tout l'espace, avec des trous dans lesquels
on peut loger exactement des tétraèdres réguliers.
On obtient donc ainsi un pavage bord à bord de l'espace par des polyèdres réguliers, avec des dispositions identiques autour des sommets (6 octaèdres et 8 tétraèdres) ; c'est donc un pavage semi-régulier de l'espace, et c'est d'ailleurs le seul, excepté le pavage par des cubes. |
 |
 |
 |
L'octaèdre régulier donne une réponse
au problème dit "des dictateurs ennemis" dans le cas n =
6 : "quelle est la taille maximale de n calottes sphériques
identiques (les états de chaque dictateur) se répartissant
sur une sphère sans se chevaucher, et quelle est alors leur disposition
?"
Réponse : les 6 calottes maximales ont un angle au centre de 90° et sont centrées aux sommets d'un octaèdre régulier. Les états occupent alors 87,9 % de la surface totale. Sources : Marcel Berger, Pour la Science 176, p. 72 et dossier Pour la Science 41 p. 40. |
 |
Les 12 arêtes de l'octaèdre se regroupent
en 3 carrés dont les plans se coupent à angles droits.
Projetés sur la sphère circonscrite, ces 3 carrés deviennent 3 grands cercles deux à deux orthogonaux, découpant un pavage régulier de la sphère par 8 triangles équilatéraux sphériques. Entrelacés alternativement "dessus-dessous", ces 3 cercles fournissent un entrelacs premier qui n'est autre que l'entrelacs des anneaux de Borromée. A droite, une version où les trois cercles ont été déformés en des ellipses, tout en restant dans leur plan. Le cuboctaèdre , l'icosidodécaèdre et le tétraki-hexaèdre présentent un phénomène similaire. |
 |
| Polyèdre composé formé de l'octaèdre et du cube dual polaire par rapport à la sphère tangente aux arêtes ; la partie commune est le cuboctaèdre. L'enveloppe des sommets est le dodécaèdre rhombique. |  |
Voir aussi l'hyperoctaèdre.

Cristal octaédrique de fluorite |

Radiolaire octaédrique dessiné par Ernst Haeckel en 1887 |
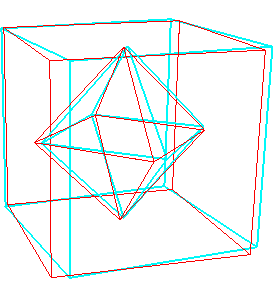
Anaglyphe à regarder avec des lunettes rouge (à gauche) et bleu (à droite). |
 |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016