polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

TETRAKI-HEXAÈDRE
Tetrakis hexahedron, Tetrakishexaeder

Famille polyèdre semi-régulier de deuxième espèce, ou polyèdre de Catalan
Historique  polyèdre connu de Képler
Étymologie du grec "tetrakis" quatre fois et hexaèdre
Autres noms tétrakihexaèdre, tétrahexaèdre, tétracube, cube à toits
Dual octaèdre tronqué
Faces 24 triangles isocèles d'angle au sommet 83° 37' 
Sommets 6 sommets de degré 4, de code de Schläfli 34, et 8 de degré 6 de code 36
Arêtes 12 arêtes de longueur 2a et 24 de longueur 3/2 a ;
angle dièdre : 
Patron et graphe
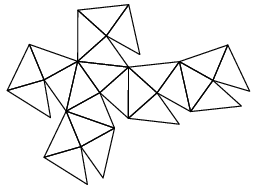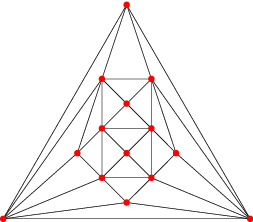Diamètres sphère inscrite : ; sphère circonscrite : 3a
Mensurations volume : 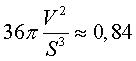 ; aire : ; coefficient isopérimétrique : 
Coordonnées 
des sommets		 et  avec leurs permutés.
Équations des 24 plans faces et ses permutés, d'où l'équation de la surface : 
Équations des 6 plans passant par O contenant les arêtes et ses permutés, d'où l'équation de la surface : .
Constructions   - dual polaire de l'octaèdre tronqué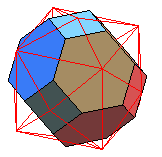
   - cube augmenté de 6 pyramides dont la hauteur (= a/2) est définie par le fait que tous les angles dièdres doivent être égaux :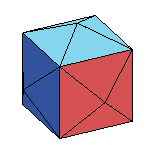
Si l'on augmente la hauteur de sorte que deux triangles contigus soient coplanaires, on obtient le dodécaèdre rhombique.
Groupe des isométries  = celui du cube
Polyède dérivé Triacontahexaède tétragonal

 
Ne pas confondre le tétraki-hexaèdre avec le polyèdre obtenu en adjoignant au cube 6 pyramides à faces équilatérales, polyèdre qui est à faces régulières mais n'est pas convexe :
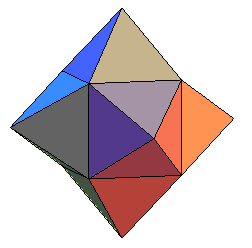Les 36 arêtes du tétracube se regroupent en 6 hexagones non réguliers, de couleurs différentes ci-contre.
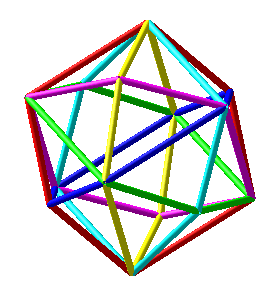Projetés sur la sphère cicconscrite, les 6 hexagones deviennent les 6 cercles ci-contre.
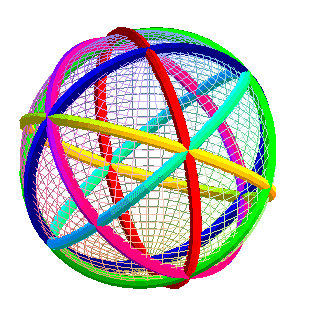Vue avec les anneaux et les hexagones.

 
 
La pyramide supérieure de la borne Michelin semble être de hauteur légèrement inférieure à celle du tétracube....

 
 
polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL 2007